트리(Tree)란
트리는 그 이름에서 알 수 있듯이 나무를 닮은 자료구조이다.
실생활에서 이러한 구조를 많이 사용하는데, 의사 결정 트리, 스킬 트리 등 여러 방면으로 많이 사용한다.
컴퓨터 과학에서도 활용도가 매우 높다.
HTML, XML 문서를 다룰 때 사용하는 DOM, PC 폴더 구조, 운영체제 파일 시스템 등도 트리 구조로 이루어져 있다.
트리의 구성 요소
트리는 크게 뿌리(Root), 가지(Branch), 잎(Leaf) 세 가지 요소로 이루어져 있다.
뿌리, 가지, 잎은 모두 똑같은 노드이지만 트리에서 어디에 위치하는지에 따라 불리는 이름이 달라진다.
뿌리는 트리 자료구조의 가장 위에 있는 노드를 가리키고, 가지는 뿌리와 잎 사이에 있는 모든 노드를 말한다.
그리고 가지의 끝에 있는(마지막) 노드를 잎 노드라고 부른다.
잎 노드는 끝에 있다고 해서 단말 노드라고도 한다.
아래와 같은 구조가 있다.
노드 B, C, D를 보면 B에서 C와 D가 뻗어 나오는데 이때 B는 C와 D의 부모(Parent)이고, C와 D는 B의 자식(Children)이다.
그리고 한 부모 밑에서 태어난 C와 D를 형제(Sibling) 라고 한다.

자식 부모 형제 구조와 더불어 경로(Path)도 중요한 정보이다.
한 노드에서 다른 한 노드까지 이르는 길 사이에 있는 노드들의 순서를 일컬어 경로라고 한다.
예를 들어 아래 그림의 B 노드에서 F 노드를 갈 때 B노드에서 출발하여 D, F에 도착한다.
이때 B -> D -> F를 B에서 F까지의 경로라고 한다.

경로에는 길이(Length) 속성이 있는데, 출발 노드에서 목적지 노드까지 거쳐야 하는 노드 개수를 말한다.
B -> D -> F의 경우는 2가 된다.(B -> D 1번, D -> F 2번)
또한 노드의 깊이(Depth)는 뿌리 노드에서 해당 노드까지 이르는 경로의 길이를 말한다.
아래 그림에서 예로 보면 G 노드는 뿌리 노드인 A로부터 이어지는 경로의 길이가 1이고 깊이도 1이다.
K노드는 A노드로부터 이어지는 경로의 길이가 3이고, 깊이도 3이다.

비슷한 개념의 용어로 레벨(Level)과 높이(Height)가 있다.
레벨은 깊이가 같은 노드의 집합을 일컫는 말이다.
앞의 그림에서 '레벨2'의 경우 C, D, H, J 전체 노드를 가리킨다. (모두 깊이가 2인 노드들)
높이는 뿌리 노드부터 잎 노드까지의 길이를 말한다.
앞의 그림에서 높이는 잎 노드(E, F, K) 부터 A까지 이므로 높이가 3이 된다.
또한 차수(Degree)라는 개념이 잇다.
노드의 차수는 그 노드의 자식 노드 개수를 뜻하고, 트리의 차수는 트리 내에 있는 노드들 가운데 자식 노드가 가장 많은 노드를 뜻한다.
다음 그림에서 A노드는 자식 노드의 개수가 3이므로 차수가 3이고, B노드는 자식 노드가 2개이므로 차수가 2이다.
트리 전체적으로 보면 가장 많은 노드가 A노드이고, A의 차수가 3이므로 트리의 차수는 3이 된다.

트리 표현 방법
트리는 다양한 방법으로 표현할 수 있는 추상 자료형 구조(ADT: Abstract Data Type)이다.
먼저 중첩된 괄호(Nested Parenthesis)로 표현할 수 있다. 이 표현법은 같은 레벨의 노드들을 괄호로 묶어 표현하는 방법이다.
예를 들어 아래와 같은 그림이 있는데, 왼쪽 트리를 중첩딘 괄호 표현법으로 표현하면 오른쪽 형식으로 표현할 수 있다.
이 경우 읽기는 다소 어렵지만 트리를 하나의 공식처럼 표현할 수 있는 것이 장점이다.

또한 중첩된 집합(Netsted Set)으로도 표현할 수 있다.
이 표현법은 트리가 하위 트리리의 집합이라는 사실을 잘 표현할 수 있는 장점이 있다.

마지막으로 들여쓰기(Indentation) 표현법으로도 트리를 표현할 수 있다.
이 방법으로 표현한 트리는 자료의 계층적인 특징을 잘 나타내며, 윈도우 탐색기의 폴더 트리와 같은 방법이다.

노드 표현 방법
노드 표현 방법은 부모와 자식, 형제 노드를 서로 연결 짓는 방법이라고 할 수 있다.
트리 노드를 표현하는 방법에는 두 가지로 N-링크(N-Link) 표현법과 왼쪽 자식 - 오른쪽 형제(Left Child - Right Sibling) 표현법이다.
N-Link 표현법
N-Link는 노드의 차수가 N이라면 노드가 N개의 링크를 갖고 있는데, 이 링크들이 각각 자식 노드를 가리키도록 노드를 구성하는 방법이다.
N-Link로 트리를 표현하면 다음과 같이 표현할 수 있다.

N-Link 표현법은 자식 노드의 수가 달라지는 트리에는 적용하기 힘들다는 단점이 있다.
에를 들어 폴더 트리 같은 경우 자식 노드의 수가 0일 수도 있고, 수백 수천일 가능성이 있다.
이런 경우 트리 구현이 상당히 복잡해진다.
왼쪽 자식 - 오른쪽 형제 표현법
이 표현법은 N-Link 표현법과 다르게 트리 구조가 복잡하더라도 표현하는데 문제가 없다.
이 표현법은 말 그대로 왼쪽 자식과 오른쪽 형제에 대한 포인터만을 갖도록 노드를 구성하는 방법이다.
이 표현법을 사용하면 N개의 차수를 가진 노드의 표현이 오로지 2개의 포인터(왼쪽 자식과 오른쪽 형제 포인터) 만으로 가능하게 된다.
이 표현법을 트리로 나타내면 아래와 같은 그림이 된다.
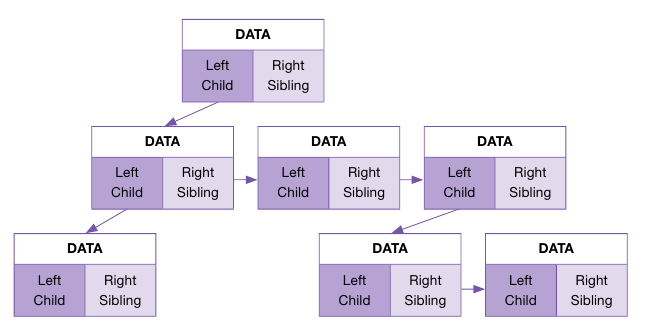
이 표현법을 사용하는 트리에서 어느 한 노드의 모든 자식 노드를 얻으려면, 일단 왼쪽 자식 노드에 대한 포인터만 있으면 된다.
해당 포인터를 이용해서 왼쪽 자식 노드의 주소를 얻은 후, 이 자식 노드의 오른쪽 형제 노드의 주소를 얻는다.
그 다음 오른쪽 형제 노드의 주소를 게속해서 얻어나가면 모든 자식의 노드를 얻을 수 있다.
트리의 기본 연산
트리의 기본 연산으로 생성, 소멸, 연결, 출력 등이 있다.
예제로는 왼쪽 자식 - 오른쪽 형제 표현법을 사용하여 트리를 표현한다.
노드 선언
왼쪽 자식 - 오른쪽 형제 표현법의 노드 구조체는 데이터를 담는 data, 왼쪽 자식 child, 오른쪅 형제 sibling을 가리키는 2개의 포인터로 구성된다.
typedef struct _Node
{
struct _Node* child;
struct _Node* sibling;
char data;
} Node;
노드 생성
노드를 생성하기 위해 먼저 동적 메모리를 생성해야 한다.
malloc() 함수를 사용하여 구조체의 크기만큼 동적 메모리 생성 후 매개 변수를 사용해 data에 저장하고, 노드의 메모리 주소를 반환한다.
Node* CreateNode(char newData)
{
// 노드 구조체 크기만큼 동적 메모리 할당
Node* newNode = (Node*)malloc(sizeof(Node));
// 루트 노드 생성
newNode->child = NULL;
newNode->sibling = NULL;
newNode->data = newData;
// 메모리 주소 반환
return newNode;
}
노드 소멸
노드 소멸은 간단하게 free() 함수를 이용해 동적 메모리 할당을 해제한다.
void DestroyNode(Node* node)
{
// 동적 메모리 할당 해제
free(node);
}
자식 노드 연결
자식 노드를 연결하기 위해 먼저 부모 노드인 Parent에게 자식 노드가 있는지 검사한다.
먼저 왼쪽 자식의 값이 NULL일 경우 자식이 없다는 것을 알 수 있다.
만약 Parent에게 자식 노드가 없을 경우 Parent의 Child 포인터에 자식 노드를 바로 저장하면 된다.
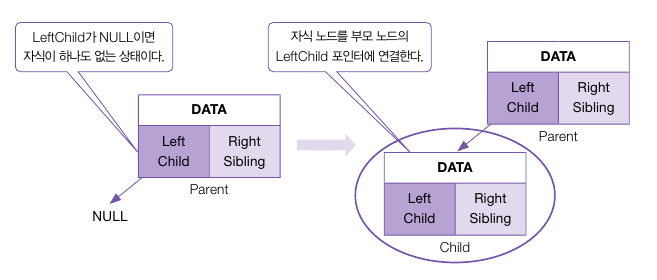
이렇게 Parent의 Child가 NULL이 아닌 경우 자식 노드를 하나 이상 갖고 있다는 의미이다.
이럴 때는 자식 노드의 sibling 포인터를 이용해 가장 오른쪽에 있는 자식 노드를 찾아내고, 찾아낸 가장 오른쪽 자식 노드의 sibling에 child를 대입한다.
이렇게 하면 Parent는 새로운 자식을 하나 더 얻게 된다.
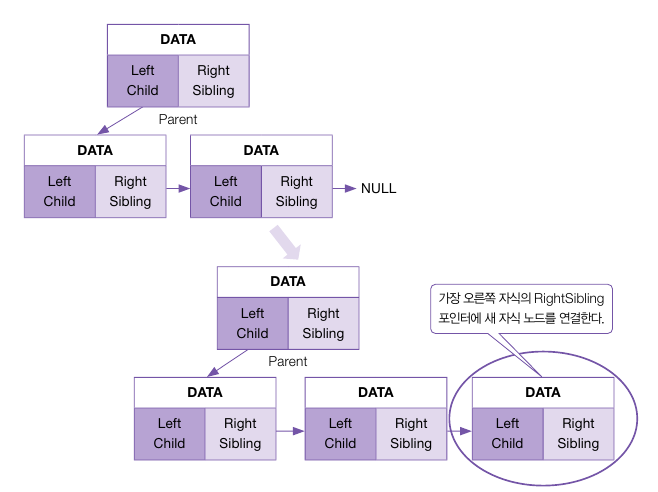
이 내용을 코드로 구현하면 아래와 같다.
void AddChildNode(Node* parent, Node* child)
{
// 자식이 하나도 없으므로 바로 연결
if(parent->child == NULL) {
parent->child = child;
}
// 자식이 있는 경우
else {
// 기존 있던 자식 노드
Node* tempNode = parent->child;
// 가장 오른쪽에 있는 자식 노드를 찾을 때까지 반복
while(tempNode->sibling != NULL) {
tempNode = tempNode->sibling;
}
tempNode->sibling = child;
}
}
트리 출력
트리를 출력은 들여쓰기 표현법으로 트리를 출력한다.
들여쓰기 표현법으로 표현 시 계층 구조를 한 눈에 볼 수 있어 직관성이 좋다.
void PrintTree(Node* node, int depth)
{
// 공백 3칸을 사용하여 들여쓰기
int i = 0;
for(i = 0;i < depth - 1; i++) {
printf(" ");
}
// 노드 자식 여부 표시
if(depth > 0) {
printf("+--");
}
// 노드 데이터 출력
printf("%c\n", node->data);
// 왼쪽 자식이 존재할 경우 재귀 반복
if(node->child != NULL) {
PrintTree(node->child, depth+1);
}
// 오른쪽 형제가 존재할 경우 재귀 반복
if(node->sibling != NULL) {
PrintTree(node->sibling, depth);
}
}
예제 코드
이 예제 코드는 아래 그림과 같은 트리 구조를 가지고 있다.
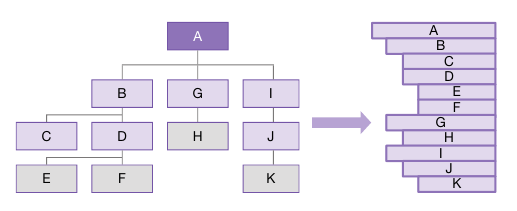
#include <stdio.h>
#include <stdlib.h>
typedef struct _Node
{
struct _Node* child;
struct _Node* sibling;
char data;
} Node;
Node* CreateNode(char newData);
void DestroyNode(Node* node);
void AddChildNode(Node* parent, Node* child);
void PrintTree(Node* node, int depth);
int main()
{
// 루트 노드 생성
Node* rootNode = CreateNode('A');
// 노드 생성
Node* B = CreateNode('B');
Node* C = CreateNode('C');
Node* D = CreateNode('D');
Node* E = CreateNode('E');
Node* F = CreateNode('F');
Node* G = CreateNode('G');
Node* H = CreateNode('H');
Node* I = CreateNode('I');
Node* J = CreateNode('J');
Node* K = CreateNode('K');
// 루트 노드 자식에 B노드 연결
AddChildNode(rootNode, B);
// B노드 자식에 C노드 연결
AddChildNode(B, C);
// B노드 자식에 D노드 연결, C노드와 형제
AddChildNode(B, D);
// D노드 자식에 E노드 연결
AddChildNode(D, E);
// D노드 자식에 F노드 연결, E노드와 형제
AddChildNode(D, F);
// 루트 노드 자식에 G노드 연결, B노드와 형제
AddChildNode(rootNode, G);
// G노드 자식에 H노드 연결
AddChildNode(G, H);
// 루트 노드 자식에 I노드 연결, B노드, G노드와 형제
AddChildNode(rootNode, I);
// I노드 자식에 J노드 연결
AddChildNode(I, J);
// J노드 자식에 K노드 연결
AddChildNode(J, K);
// 노드 출력
PrintTree(rootNode, 0);
// 노드 소멸
DestroyNode(rootNode);
return 0;
}
Node* CreateNode(char newData)
{
// 노드 구조체 크기만큼 동적 메모리 할당
Node* newNode = (Node*)malloc(sizeof(Node));
// 루트 노드 생성
newNode->child = NULL;
newNode->sibling = NULL;
newNode->data = newData;
// 메모리 주소 반환
return newNode;
}
void DestroyNode(Node* node)
{
// 동적 메모리 할당 해제
free(node);
}
void AddChildNode(Node* parent, Node* child)
{
// 자식이 하나도 없으므로 바로 연결
if(parent->child == NULL) {
parent->child = child;
}
// 자식이 있는 경우
else {
// 기존 있던 자식 노드
Node* tempNode = parent->child;
// 가장 오른쪽에 있는 자식 노드를 찾을 때까지 반복
while(tempNode->sibling != NULL) {
tempNode = tempNode->sibling;
}
tempNode->sibling = child;
}
}
void PrintTree(Node* node, int depth)
{
// 공백 3칸을 사용하여 들여쓰기
int i = 0;
for(i = 0;i < depth - 1; i++) {
printf(" ");
}
// 노드 자식 여부 표시
if(depth > 0) {
printf("+--");
}
// 노드 데이터 출력
printf("%c\n", node->data);
// 왼쪽 자식이 존재할 경우 재귀 반복
if(node->child != NULL) {
PrintTree(node->child, depth+1);
}
// 오른쪽 형제가 존재할 경우 재귀 반복
if(node->sibling != NULL) {
PrintTree(node->sibling, depth);
}
}
실행 결과
A
+--B
+--C
+--D
+--E
+--F
+--G
+--H
+--I
+--J
+--K
출처 : Do it! 자료구조와 함께 배우는 알고리즘 입문: C 언어 편
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] C - 수식 트리(Expression Tree) (1) | 2022.12.04 |
|---|---|
| [Algorithm] C - 이진 트리(Binary Tree) (0) | 2022.12.04 |
| [Algorithm] C - 이진 탐색 트리(Binary Search Tree) (4) | 2022.12.03 |
| [Algorithm] C++ - 소수 구하기 (제곱근, 에라토스테네스의 체) (0) | 2022.11.20 |
| [Algorithm] C++ - 10진수, 2진수 진법 변환 (0) | 2022.11.20 |