[Algorithm] C - 이진 탐색 트리(Binary Search Tree)

Algorithm/이론

[Algorithm] C - 이진 탐색 트리(Binary Search Tree)

유제필 2022. 12. 3. 16:34

이진 탐색 트리 요약

시간 복잡도 : O(log(n)) ~ O(n)

왼쪽 하위 트리는 루트보다 작은 값이 위치함
오른쪽 하위 트리는 루트보다 큰 값이 위치함
정렬되어 있는 트리 구조에서 빠른 탐색 속도를 보임
한쪽으로 편향되어 있는 트리 구조에서 비효율적임

이진 탐색 트리(Binary Search Tree)

이진 탐색 트리란 트리 내부에 있는 노드의 값을 찾는 방법으로 아래와 같이 3가지의 조건을 만족하면 된다.

각 노드는 왼쪽 자식 노드보다 큼
각 노드는 오른쪽 자식보다 작음
같은 키 값을 갖는 노드는 없음

위 그림은 이진 탐색 트리를 구현한 예이다.
여기서 노드 5를 보면 왼쪽 하위 트리 노드(4, 1)은 모두 5보다 작다. (조건 1번에 해당)
그리고 오른쪽 하위 트리 노드(7, 6, 9)는 모두 5보다 크다. (조건 2번에 해당)

이때 이진 탐색 트리를 중위 순회(Inorder)하면 다음과 같이 키 값의 오름차순으로 노드를 얻을 수 있다.

1 -> 4 -> 5 -> 6 -> 7 -> 9 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18

이와 같이 이진 탐색 트리는 중위 순회를 하면 몇 가지의 장점이 있어 자주 사용된다.

키 값의 오름차순으로 노드를 얻을 수 있음
구조가 단순하여 구현이 쉬움
이진 탐색과 비슷한 방식으로 탐색 가능
노드의 삽입이 용이함

이진 트리에서의 이진 탐색

이진 트리 탐색에서 가장 중요한 전제 조건은 이진 탐색이 가능한 상태로 정렬되어 있어야 한다.
(이진 탐색도 배열이 정렬되어 있어야 탐색이 가능한 것 처럼)

이진 트리에서 탐색을 하기 위해 이진 탐색 트리의 가장 중요한 아래 조건을 알고 있어야 한다.

각 노드는 왼쪽 자식 노드보다 큼
각 노드는 오른쪽 자식보다 작음
같은 키 값을 갖는 노드는 없음

여기서 중요한 점은 각 노드는 왼쪽 자식보다 크고 오른쪽 자식보다 작은데, 이 각 노드를 중앙 요소라고 한다.
예를 들어 아래와 같은 트리가 있다.

위 트리에서 루트 노드는 23이고, 23은 트리 전체의 중앙 요소이다.
23 노드의 왼쪽에는 23보다 작은 값들만 있고, 오른쪽에는 23보다 큰 값들만 존재한다.

하위 트리로 내려가도 같은 규칙이 적용되고 있다.
23 노드 왼쪽 하위 트리의 노드는 11인데, 11 노드의 왼쪽에는 작은 값(1), 오른쪽에는 큰 값(14)가 있다.

마찬가지로23 노드 오른쪽 하위 트리의 노드도 같은 규칙이 적용되어 있다.

이처럼 중앙 요소를 찾아 좌우의 대소를 비교하여 탐색 범위를 정하고, 또 다시 중앙 요소를 찾아 좌우의 대소를 비교하는 일을 반복한다.
이렇게 보면 배열에서 이진 탐색을 하는 것과 동일하다.

이진 트리 노드 탐색 과정

아래 예제가 트리에서 67을 찾는 과정이다.

먼저 루트 노드인 23 노드와 목표값 67을 비교한다.
비교 시 목표 값이 더 큰 것을 알 수 있으며, 이 경우 왼쪽을 버리고 오른쪽으로 탐색 대상을 좁히고 다시 탐색한다.

139는 67보다 크므로 중앙 요소인 139 노드를 기준으로 오른쪽을 버리고 다시 왼쪽으로 탐색 대상을 좁힌다.

왼쪽 노드를 확인해 보니 찾고자 하는 67과 같은 값인 것을 확인할 수 있다.

이진 트리 노드 삽입 과정

이진 트리 삽입 과정 중 노드 삽입 연산의 핵심은 새 노드가 삽입될 곳이 어디인지를 찾아내는 부분이다.
즉, 새 노드가 삽입될 곳을 이진 탐색으로 찾아내야 한다.

이진 탐색으로 새 노드를 연결할 부모 노드를 찾아낸 후 그곳에 노드를 놓으면 노드 삽입 연산이 완료된다.

예를 들어 아래 예제로 트리에서 14를 삽입하는 과정을 나타낸다.

14는 23보다 작으므로 23의 왼쪽 하위 트리에 위치해야 하고, 11보다 크므로 11의 오른쪽 하위 트리에 위치해야 한다.

이진 트리 노드 삭제 과정

이진 트리에서 노드를 삭제하기 위해 먼저 삭제할 노드를 찾아야 한다.
이 작업은 이진 탐색을 통해 찾으며, 탐색 이후 노드가 어디에 있는지 알아내고, 그 노드를 삭제한다.

이때 삭제하는 노드가 잎 노드(Leaf Node)라면 문제 없이 부모 노드에서 자식 노드의 포인터를 NULL로 주고, 삭제한 노드의 주소를 반환하면 작업이 마무리 된다.

아래 예제는 이진 트리에서 14 노드를 제거하는 과정을 나타낸다.
14 노드는 자식이 없으므로 그냥 트리에서 해당 노드를 삭제하고, 11의 오른쪽 자식 노드를 NULL로 초기화하면 된다.

위 처럼 자식이 없을 경우는 간단하지만, 자식이 있는 경우는 조금 더 복잡해진다.
자식 노드가 있을 경우에도 두 가지로 나뉜다.

양쪽 자식 노드를 모두 갖고 있는 경우
왼쪽과 오른쪽 중 어느 한쪽 자식 노드만 갖고 있는 경우

먼저 두 번째 경우인 한쪽 자식만 가진 노드를 처리하는 부분은 양쪽 자식이 있을 경우보다 상대적으로 간단하다.
삭제할 노드의 자식을 삭제할 노드의 부모에 연결만 시키면 된다.

아래 그림은 한쪽 자식의 노드를 삭제하는 과정으로, 139 노드를 삭제한다.
그 후 해당 노드를 가리키던 부모 노드(23)의 오른쪽 자식 포인터를 67 노드에 연결한다.

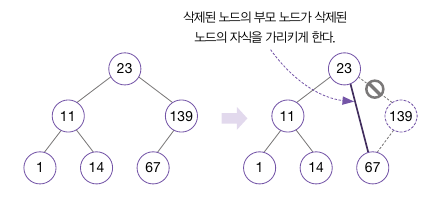
위와 같이 한쪽 자식이 있을 경우는 간단하게 마무리 되었지만, 양쪽 자식이 있는 경우는 다르다.
아래 그림은 양쪽 자식이 있는 경우이며, 11을 삭제하는 경우이다.

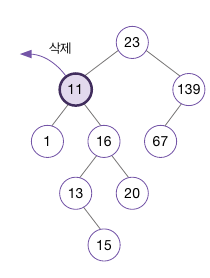
먼저 삭제된 노드의 오른쪽 하위 트리에서 가장 작은 값을 가진 노드(최솟값 노드)를 삭제된 노드의 위치에 옮겨놓는다.
삭제된 11노드의 오른쪽 하위 트리에서 가장 작은 13 노드를 옮겨 11 노드가 있던 자리에 놓는다.

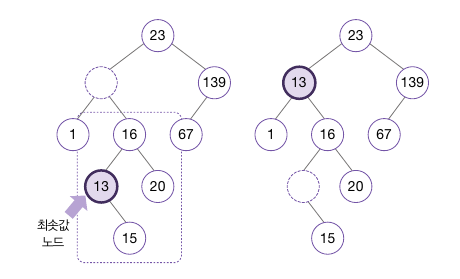
옮겨 놓은 최솟값 노드가 자식이 없는 경우라면 이렇게 노드를 빈자리에 옮겨 놓는 것만으로 작업이 완료된다.
하지만 자식이 있는 경우 추가 작업을 해주어야 한다.

추가 작업이 필요한 이유는 왼쪽 자식이 있으면 자기보다 작은 값을 가진 노드가 하위 트리에 있다는 뜻인데,
이렇게 되면 최솟값 노드가 더 이상 최솟값 노드가 아니게 되기 때문이다.

마지막으로 최솟값 노드의 오른쪽 자식을 최솟값 노드의 원래 부모에게 연결하면 삭제 작업이 모두 완료된다.
이 경우는 15 노드를 16 노드의 왼쪽 자식으로 만들면 된다.

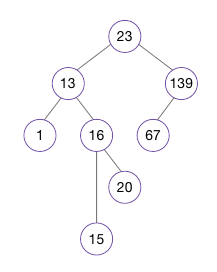
이진 탐색 트리의 문제점

이진 탐색 트리는 정렬되어 있는 데이터 구조에서는 탐색 속도도 빠르고 잘 처리할 수 있지만, 기형적인 데이터 구조에서는 효율이 많이 떨어진다.

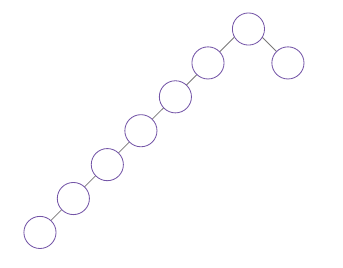
이 경우 Red-Black 트리 또는 AVL 트리로 해결해야 한다.

예제 코드

#include <stdio.h>
#include <stdlib.h>

typedef struct _Node
{
    struct _Node* left;
    struct _Node* right;
    int data;
} Node;

// 새로운 노드 생성
Node* CreateNode(int newData);

// 노드 삭제
void DestroyNode(Node* node);

// 트리 삭제
void DestoryTree(Node* tree);

Node* SearchNode(Node* tree, int target);
Node* SearchMinNode(Node* tree);
void InsertNode(Node* tree, Node* child);
Node* RemoveNode(Node* tree, Node* parent, int target);
void InorderPrintTree(Node* Node);
void PrintSearchResult(int target, Node* result);

int main() 
{
        // 신규 트리 및 노드 생성
    Node* tree = CreateNode(123);
    Node* node = NULL;
    
    // 트리에 노드 추가
    InsertNode(tree, CreateNode(22));
    InsertNode(tree, CreateNode(9918));
    
    InsertNode(tree, CreateNode(424));
    InsertNode(tree, CreateNode(17));
    InsertNode(tree, CreateNode(3));
    
    InsertNode(tree, CreateNode(98));
    InsertNode(tree, CreateNode(34));
    
    InsertNode(tree, CreateNode(760));
    InsertNode(tree, CreateNode(317));
    InsertNode(tree, CreateNode(1));

    int target = 17;
    
    node = SearchNode(tree, target);
    PrintSearchResult(target, node);
    
    target = 117;
    node = SearchNode(tree, target);
    PrintSearchResult(target, node);
    
    // 트리 출력
    InorderPrintTree(tree);
    
    // 특정 노드 삭제
    printf("\nRemove 98 Node\n");
    
    node = RemoveNode(tree, NULL, 98);
    DestroyNode(node);
    
    InorderPrintTree(tree);
    printf("\n");
    
    // 신규 노드 삽입
    printf("Insert 111 Node\n");
    
    InsertNode(tree, CreateNode(111));
    InorderPrintTree(tree);
    
    // 트리 제거
    DestoryTree(tree);
    
    return 0;
}

Node* CreateNode(int newData)
{
    Node* newNode = (Node*)malloc(sizeof(Node));
    
    // 루트 노드 생성 및 왼쪽 오른쪽 초기화
    newNode->left = NULL;
    newNode->right = NULL;
    newNode->data = newData;
    
    return newNode;
}

void DestoryNode(Node* node)
{
    free(node);
}

void DestroyTree(Node* tree)
{
    // 오른쪽 하위 트리가 있을 경우 재귀 호출하여 오른쪽 하위 트리 삭제
    if(tree->right != NULL) {
        DestroyTree(tree->right);
    }
    
    // 왼쪽 하위 트리가 있을 경우 재귀 호출하여 왼쪽 하위 트리 삭제
    if(tree->left != NULL) {
        DestroyTree(tree->left);
    }
    
    // 모든 트리 삭제
    tree->left = NULL;
    tree->right = NULL;
    
    // 루트 노드 삭제
    DestroyNode(tree);
}

Node* SearchNode(Node* tree, int target)
{
    // 빈 트리일 경우
    if(tree == NULL) {
        return NULL;
    }
    
    // 노드의 값을 찾았을 경우
    if(tree->data == target) {
        return tree;
    }
    
    // 데이터가 찾고자 하는 값보다 낮을 경우, 왼쪽 하위 트리 탐색
    else if(tree->data > target) {
        return SearchNode(tree->left, target);
    }
    
    // // 데이터가 찾고자 하는 값보다 클 경우, 오른쪽 하위 트리 탐색
    else {
        return SearchNode(tree->right, target);
    }
}

Node* SearchMinNode(Node* tree)
{
    // 빈 트리일 경우
    if(tree == NULL) {
        return NULL;
    }
    
    // 왼쪽 자식이 없을 경우, 즉 가장 작은 값일 경우
    if(tree->left == NULL) {
        return tree;
    }
    
    // 왼쪽 하위 노드를 계속해서 탐색
    else {
        return SearchMinNode(tree->left);
    }
}

void InsertNode(Node* tree, Node* child)
{
    // 중앙 요소 노드가 넣고자 하는 노드보다 작을 때, 즉 큰 값의 경우
    if(tree->data < child->data) {
        
        // 트리의 가장 오른쪽에 삽입
        if(tree->right == NULL) {
            tree->right = child;
            
        } 
        
        // 트리의 가장 오른쪽까지 재귀
        else {
          InsertNode(tree->right, child);
            
        }
    }
    
    // 중앙 요소 노드가 넣고자 하는 노드보다 클 때, 즉 작은 값의 경우
    else if(tree->data > child->data) {
        
        // 트리의 가장 왼쪽에 삽입
        if(tree->left == NULL) {
            tree->left = child;
        }
        
        // 트리의 가장 왼쪽까지 재귀
        else {
            InsertNode(tree->left, child);
        }
    }
}

Node* RemoveNode(Node* tree, Node* parent, int target)
{
    Node* removeNode = NULL;
    
    // 빈 트리일 경우
    if(tree == NULL) {
        return NULL;
    }
    
    // 삭제할 값보다 클 경우 왼쪽 하위 트리 계속 탐색
    if(tree->data > target) {
        removeNode = RemoveNode(tree->left, tree, target);
    }
    
    // 삭제할 값보다 작을 경우 오른쪽 하위 트리 게속 탐색
    else if(tree->data < target) {
        removeNode = RemoveNode(tree->right, tree, target);
    }
    
    // 목표 값을 찾은 경우
    else {
        removeNode = tree;
        
        // Leaf 노드인 경우 바로 삭제
        if(tree->left == NULL && tree->right == NULL) {
            if(parent->left == tree) {
                parent->left = NULL;
            }
            else {
                parent->right = NULL;
            }
        }
        
        else {
            // 자식이 양쪽에 다 있는 경우
            if(tree->left != NULL && tree->right != NULL) {
                // 최솟값 노드를 찾아 제거 후 현재 노드에 위치 시킴
                Node* minNode = SearchMinNode(tree->right);
                
                minNode = RemoveNode(tree, NULL, minNode->data);
                
                tree->data = minNode->data;
            }
            
            else {
                // 자식이 한쪽만 있는 경우
                Node* temp = NULL;
                
                // 자식이 왼쪽일 경우
                if(tree->left != NULL) {
                    temp = tree->left;
                }
                // 자식이 오른쪽일 경우
                else {
                    temp = tree->right;
                }
                
                // 부모 위치에 따라 값 교환
                if(parent->left == tree) {
                    parent->left = temp;
                }
                else {
                    parent->right = temp;
                }
            }
        }
    }
    
    return removeNode;
}

void InorderPrintTree(Node* node)
{
    // 빈 트리일 경우
    if(node == NULL) {
        return;
    }
    
    // 왼쪽 하위 트리 출력
    InorderPrintTree(node->left);
    
    // 루트 노드 출력
    printf("%d ", node->data);
    
    // 오른쪽 하위 노드 출력
    InorderPrintTree(node->right);
}

void PrintSearchResult(int target, Node* result)
{
    if(result != NULL) {
        printf("찾은 노드 : %d \n", result->data);
    }
    else {
        printf("노드가 없습니다. %d\n", target);
    }
}

실행 결과

찾은 노드 : 17 
노드가 없습니다. 117
1 3 17 22 34 98 123 317 424 760 9918 
Remove 98 Node
1 3 17 22 34 123 317 424 760 9918 
Insert 111 Node
1 3 17 22 34 111 123 317 424 760 9918

https://github.com/JeHeeYu/Algorithm/tree/main/Tree/Binary%20Search%20Tree

GitHub - JeHeeYu/Algorithm: 알고리즘 개념 및 문제 풀이

알고리즘 개념 및 문제 풀이. Contribute to JeHeeYu/Algorithm development by creating an account on GitHub.

github.com

출처 : Do it! 자료구조와 함께 배우는 알고리즘 입문: C 언어 편

'Algorithm > 이론' 카테고리의 다른 글

[Algorithm] C - 이진 트리(Binary Tree) (0)	2022.12.04
[Algorithm] C - 트리(Tree) 자료 구조 (0)	2022.12.04
[Algorithm] C++ - 소수 구하기 (제곱근, 에라토스테네스의 체) (0)	2022.11.20
[Algorithm] C++ - 10진수, 2진수 진법 변환 (0)	2022.11.20
[Algorithm] C - Boyer-Moore 문자열 검색 알고리즘 (1)	2022.11.19

현재글[Algorithm] C - 이진 탐색 트리(Binary Search Tree)

임베디드 개발자 유제필의 블로그 입니다.

OpenCV, arm, Flutter, DART, Computer Vision, C, Mat 클래스, 알고리즘, 트리, STM32, C언어, 자료구조, Embedded, 문자열 검색, 백준, 임베디드, c++, Linux, 정렬, Baekjoon,

Today :
Yesterday :

유제필의 개발 블로그