소수(Prime Number)란
소수란 1보다 큰 자연수 중 1과 자기 자신만을 약수로 가지는 수를 말한다.
아래 표는 100 이하의 소수를 나타내는 표로, 1과 자기 자신 말고 약수가 존재하지 않는다.
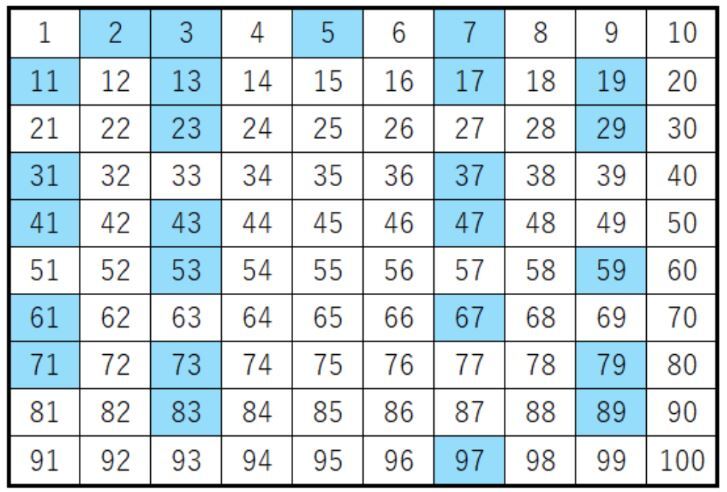
총 3가지의 방법으로, 일반 반복문, 제곱근, 에라토스테네스의 체를 이용한 방법을 설명한다.
1. 모든 경우의 수를 전부 나누는 방법 O(n)
이 경우는 판단하는 수를 2부터 그 수까지 모두 나누는 방법이다.
모든 값을 하나하나 약수가 있는지 판단하는 알고리즘으로 구현은 쉽지만 시간 복잡도가 O(n)으로 가장 비효율적이다.
bool PrimeNumber(int number)
{
for(int i = 2; i < number; i++) {
// 1개라도 나누어 떨어지면 약수가 존재하므로 false
if(number % i == 0) {
return false;
}
}
// 나누어 떨어지는 값이 없으면 소수로 판단
return true;
}
2. 제곱근을 이용해 나누는 방법 O(√n)
이 경우 모든 경우의 수를 판단하는 방법보다 효율적인 알고리즘으로, 1/2 제곱만큼 검사 시간이 줄어든다.
제곱근이란 수학에서 어떤 수의 제곱근근 제곱하여 그 수가 되는 수를 가리키는 말이다.
쉽게 말해 약수가 존재하는 수라고 할 수 있다. (9제곱근은 3으로 3제곱은 9이다.)
제곱근을 이용하기 위해서 1번의 경우와 크게 다르지 않는데, 반복 조건을 sqrt(n)을 이용하면 된다.
sqrt 함수는 에 존재하므로 #include 를 해주어야 한다.
#include
bool PrimeNumber(int number)
{
for(int i = 2; i < sqrt(number); i++) {
// 1개라도 나누어 떨어지면 약수가 존재하므로 false
if(number % i == 0) {
return false;
}
}
// 나누어 떨어지는 값이 없으면 소수로 판단
return true;
}
3. 에라토스테네스의 체(Sieve of Eratosthenes) O(n log(logn))
고대 그리스의 수학자 에라토스테네스가 만들어낸 소수 찾는 방법으로, 소수 알고리즘 중 가장 효율적인 알고리즘이다.
이 방법은 마치 조리기구 체로 치듯이 수를 걸러낸다고 하여 에라토스테네스의 체 라고 부른다.
계산 방법
먼저 1부터 100까지의 수를 나열한다.

그 후 소수도 아닌 합성수도 아닌 1을 제거한다.

다시 2를 제외한 2의 배수를 모두 제거한다.
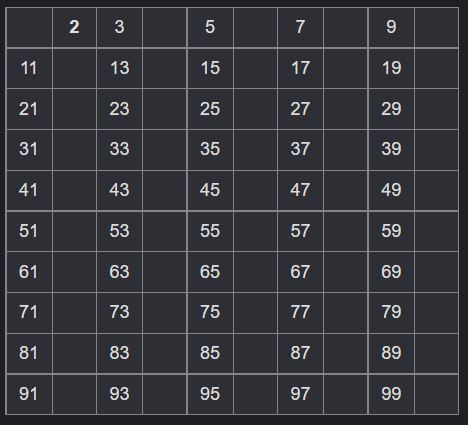
다시 3을 제외한 3의 배수를 모두 제거한다.

다시 5를 제외한 5의 배수를 모두 제거한다.
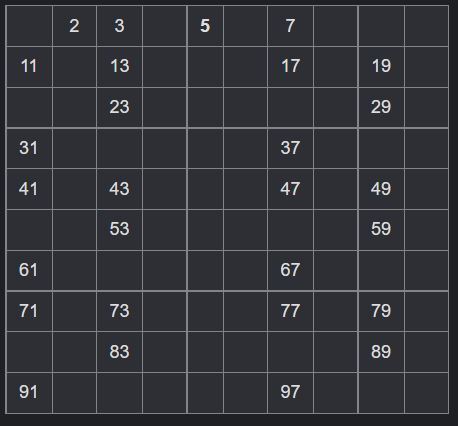
다시 7을 제외한 7의 배수를 모두 제거한다.
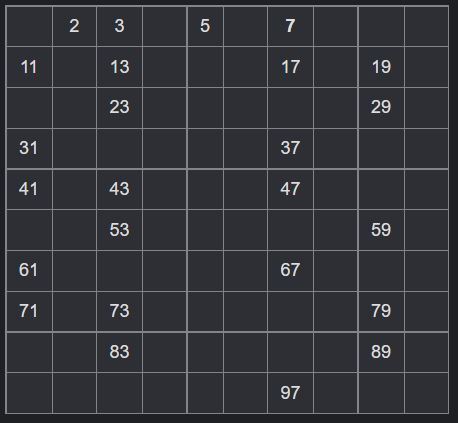
이렇게 제거하면, 4, 8, 9 등등 2나 3의 배수였던 수들이 모두 제거되므로 소수만 판별할 수 있게 된다.
다만 이 방법은 '특정 범위 내의 소수'를 판정하는 데에만 효율이 좋으므로 범위가 존재하지 않을 경우 다른 알고리즘이 더 효율적일 수 있다.
bool PrimeNumber(int number)
{
// n이하(포함) 이므로 + 1 까지 동적 할당
bool *isPrime = new bool[number + 1];
// 먼저 모든 값을 true로 초기화
for(int i = 0; i < number; i++) {
isPrime[i] = true;
}
for(int i = 2; i < number; i++) {
// 소수일 경우 해당 수를 제외한 배수들을 모두 제외
if(isPrime[i] == true) {
// 소수 출력
cout << i << endl;
// 소수 일 경우 *2 씩 하여 모든 값을 false로 할당
for(int j = i * 2; j <= number; j += i) {
isPrime[j] = false;
}
}
전체 코드
https://github.com/JeHeeYu/Algorithm/tree/main/Math/Prime%20Number
GitHub - JeHeeYu/Algorithm: 알고리즘 개념 및 문제 풀이
알고리즘 개념 및 문제 풀이. Contribute to JeHeeYu/Algorithm development by creating an account on GitHub.
github.com
출처 : 나무위키
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] C - 트리(Tree) 자료 구조 (0) | 2022.12.04 |
|---|---|
| [Algorithm] C - 이진 탐색 트리(Binary Search Tree) (4) | 2022.12.03 |
| [Algorithm] C++ - 10진수, 2진수 진법 변환 (0) | 2022.11.20 |
| [Algorithm] C - Boyer-Moore 문자열 검색 알고리즘 (1) | 2022.11.19 |
| [Algorithm] C - KMP(Knuth-Morris-Pratt Algorithm) 알고리즘 (0) | 2022.11.19 |