요약
- 해시란 다양한 길이를 가진 데이터를 고정된 길이를 가진 데이터로 매핑한 값을 말함
- 해시 테이블이란, 키와 밸류를 한 쌍으로, 해싱 함수에 따라 효율이 달라짐
- 충돌이란 데이터를 넣어야 할 주소에 이미 다른 값이 저장되어 있는 현상을 말하며 충돌 시 체이닝 기법을 적용함
- 체이닝이란 해시 함수가 충돌이 발생하면, 각 데이터를 해당 주소에 있는 링크드 리스트로 삽입하여 문제를 해결하는 기법을 말함
- 체이닝의 성능 개선으로 선형 탐사, 제곱 탐사, 이중 해싱 등이 있음
- 제일 좋은 성능은 이중 해싱으로, 해싱 함수를 두 가지를 두고, 충돌 시 두 번째 해싱 함수를 사용
해시(Hash)
해시란 다양한 길이를 가진 데이터를 고정된 길이를 가진 데이터로 매핑(Mapping)한 값이다.
즉, 해시는 데이터를 입력받아 완전히 다른 모습의 데이터로 바꾸는 작업을 말한다.
해시를 이용하여 탐색 알고리즘인 해시 테이블 알고리즘, SHA, MD5 암호화 알고리즘, 데이터 축약 등과 같은 용도로 사용한다.
해시 테이블(Hash Table)
해시 테이블이란 쉽게 말해 데이터의 해시(Hash)값을 얻어 테이블 내의 주소로 사용하는 것이다.
테이블을 (Key, Value) 구조로 데이터를 저장하는 자료구조 중 하나로, 빠르게 데이터를 검색할 수 있는 것이 장점이다.
예를 들어 배열을 선언하면 메모리에 일정 크기의 메모리가 생성된다.
그리고 각 요소에 값이 있을 때, [n]같이 접근하여 값을 가져올 수 있는데, 이 값이 커질 경우 탐색하는 시간이 많이 소요된다.
배열에서 특정 값을 찾기 위해 탐색 알고리즘을 사용하면, 탐색하는 비용이 발생하며 값을 찾아야 한다.
이 경우 배열의 크기가 커질 수록 시간이 오래 걸리는 단점이 있다.
이러한 단점을 해결하기 위해 사용하는 것이 해시 테이블 알고리즘이다.
배열에 각각의 인덱스에 해시를 매핑하여 탐색하는 비용을 줄이고, 굉장히 빠르게 찾을 수 있다.
이렇게 극한의 성능이 요구되는 분야(예 금융)에서 해시 테이블 알고리즘을 사용하며, 빠른 알고리즘(예 이분 탐색)보다 더욱 좋은 효율을 낼 수 있다.
해시 테이블에서 데이터가 해시 함수를 거치면 아래 그림처럼 테이블 내의 주소(인덱스)로 변환된다.

위 그림과 같이 123817 이라는 데이터를 해싱 함수를 거쳐 얻은 테이블 내의 주소값은 3819이다.
이제 해당 테이블 안에 해당 주소에 데이터를 저장하고, 읽을 수 있게된다.
// 데이터 저장
Table[3819] = 123817;
// 데이터 읽기
printf("Table[3819]"); // 123817 출력
위 과정을 3가지 순서로 정리할 수 있으며, 아래 그림과 같은 순서로 동작하는 개념이다.

여기서 알 수 있는 해시 테이블의 중요 개념은 데이터를 담을 테이블을 미리 크게 확보한 후 입력 받은 데이터를 해싱하여 테이블 내 주소를 계산하고 이 주소를 데이터에 담는 것이다.
해시 함수(Hash Function)
해시 함수란 입력값에서 테이블 내의 주소를 계산하는 함수를 말한다.
해시 함수 종류
해시 함수의 몇몇 예이며, 이 말고도 여러 함수가 존재한다.
- 나눗셈법 or 제산법(Division)
- 제곱법(Mid – Square)
- 숫자 분석법(Digit Analysis)
- 이동법(Shifting)
- 기수 변환법(Radix Conversion)
- 중첩법(Folding)
- 난수 생성법(Pseudo Random)
나눗셈법(Division Method) 해시 함수
나눗셈법은 해시 함수 중에서도 가장 간단한 알고리즘으로 꼽힌다.
나눗셈법은 말 그대로 입력값을 테이블의 크기로 나누고 나머지 값을 테이블의 주소로 사용한다.
주소 = 입력값 % 테이블의 크기
어떤 값이든 테이블의 크기로 나누면 그 나머지는 테이블의 크기를 절대 넘지 않는다.
입력값이 테이블 크기의 배수 또는 약수인 경우 해시 함수는 0을 반환하고, 그렇지 않은 경우 최대 n - 1을 반환한다.
즉, 나눗셈법은 0 ~ n - 1 사이의 주소 반환을 보장한다.
해싱 방법
나눗셈법은 구현이 가장 간단하다고 했는데, 코드로도 정말 간단하다.
int Hash(int input, int tableSize)
{
return input % tableSize;
}
입력값을 테이블의 크기로 나누고, 이 값을 반환하면 해시 함수 완성이다.
나눗셈법으로 구현된 해시 함수를 효율적으로 사용하기 위해서는 테이블의 크기 n을 소수(Prime Number)로 정하는 것이 좋다고 알려져 있고, 그 중에서 특히 2의 제곱수와 거리가 먼 소수를 사용하는 것이 해시 함수의 좋은 성능을 낸다.
이만큼 구현이 간단하지만, 충돌이 발생할 가능성이 높아 효율적인 해시 알고리즘은 아니다.
자릿수 접기(Digits Folding) 해시 함수
프로그래밍을 하다보면, 서로 다른 입력값에 대해 동일한 해시값을 반환할 가능성이 있다.
즉, 해시 테이블 내의 동일한 주소를 반환할 가능성이 높다는 얘기다.
이것을 충돌(Collision) 이라고 하는데, 똑같은 해시값이 아니더라도 해시 테이블 내 일부 지역의 주소들을 집중적으로 반환함으로써 데이터가 한 곳에 모이는 문제인 클러스터(Cluster)가 발생할 가능성이 높다.
이 자릿수 접기 방법을 이용하면 충돌이나 클러스터링 문제에 대해 문제를 일으킬 가능성을 줄일 수 있다.
(충돌이나 클러스터링을 완벽하게 해결하는 알고리즘은 현재 없다..)
자릿수 접기는 숫자의 각 자리수를 더해 해시값을 만드는 방법이다.
예를 들어 7자리의 수인 8129335 값이 존재한다고 하자.
8129335
이 수의 각 자리수를 모두 더하면 새로운 값인 31이 나온다.
31 = 8 + 1 + 2 + 9 + 3 + 3 + 5
또 다른 방법으로, 8129335를 2자리씩 잘라서 더해보자.
148 = 81 + 29 + 33 + 5
이처럼 자릿수 접기 방법을 통하여 일정한 범위 내의 해시값을 얻는 것을 볼 수 있다.
10진수의 경우 모든 수는 각 자리마다 0 ~ 9 까지의 값을 가질 수 있으므로, 7자리에 대해 자릿수 접기 방법을 적용한다.
한 자리씩 접으면 최소 0부터 최대 63(9 + 9 + 9 + 9 + 9 + 9 + 9 총 7자리) 까지의 해시값을 얻을 수 있고,
두 자리씩 접으면 최소 0부터 최대 306(99 + 99 + 99 + 9 총 7자리)까지의 해시값을 얻을 수 있다.
자릿수 접기는 문자열을 키로 사용하는 해시 테이블에 특히 잘 어울리는 알고리즘이다.
문자열의 각 요소를 ASCII 코드 번호로 바꾸고, 이 값을을 각각 더해서 접으면 문자열을 깔끔하게 해시 테이블의 주소로 바꿀 수 있기 때문이다.

충돌 해결 기법
충돌이란 해시 함수가 서로 다른 입력값에 대해 동일한 해시 테이블 주소를 반환하는 것을 말한다.
자릿수 접기 알고리즘을 포함한 모든 해시 함수들은 충돌을 피할 수 없지만, 체이닝 기법을 통해 조취를 취하고 있다.
해시 테이블의 충돌을 해결하는 방법은 크게 두 가지로, 개방 해싱(Open Hashing)과 폐쇄 해싱(Closed Hashing) 방법이 있다.
- 개방 해싱 : 해시 테이블의 주소 바깥에 새로운 공간을 할당하여 문제를 해결
- 주어진 해시 테이블의 공간 안에서 문제를 해결
개방 해싱을 이용한 체이닝(Chaining)
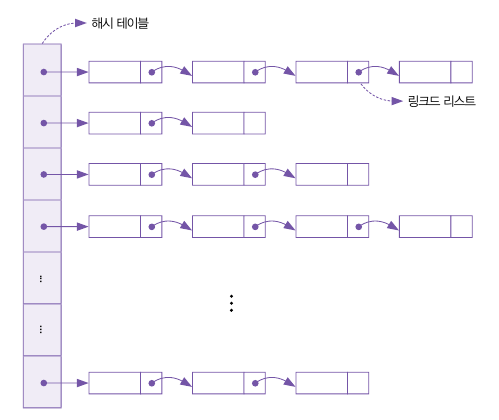
체이닝이란 해시 함수가 서로 다른 키에 대해 같은 주소값을 반환해서 충돌이 발생하면, 각 데이터를 해당 주소에 있는 링크드 리스트로 삽입하여 문제를 해결하는 기법을 말한다.
아래 그림이 체이닝의 예로, 체이닝 기반 해시 테이블은 데이터 대신 링크드 리스트에 대한 포인터를 관리한다.
이후 데이터는 해시 테이블의 각 요소가 가리키는 링크드 리스트에 저장된다.
이렇게 해시 테이블 외부에 데이터를 저장하는 체이닝은 개방 해싱 알고리즘에 해당한다.
체이닝을 이용하여 해시 테이블 알고리즘을 설계할 때 중요한 부분이 해시 테이블에 삽입하고 탐색, 삭제하는 연산 과정이다.
- 탐색 연산 : 이미 발생한 충돌을 고려하여 설계
- 삭제 연산 : 이미 발생한 충돌을 고려하여 설계
- 삽입 연산 : 앞으로 발생할 충돌을 고려해서 설계
개방 주소법(Open Addressing)
개방 주소법이란 해시 테이블에서 충돌이 일어날 때 해시 함수에 의해 만들어진 주소가 아니더라도, 다른 주소를 사용할 수 있도록 허용하는 충돌 해결 알고리즘을 말한다.
개방 주소법은 충돌이 일어나면 새로운 주소를 탐색하여 충돌된 데이터를 입력하는 방식으로 동작한다.
개방 주소법은 탐사가 전부이며, 선형 탐사, 제곱 탐사 등이 있다.
선형 탐사(Linear Probing)
선형 탐사는 가장 간단한 탐색 방법으로, 해시 함수로 얻어낸 주소에 데이터가 있을 경우 다음 주소를 탐사하여 저장할 주소를 찾는 방법을 말한다.
여기서 저장할 주소를 찾는 방법이 말 그대로 선형적인 방법으로 찾는 탐사 방법으로, 해당 주소에 데이터가 있으면 다음 주소, 그 다음 주소에도 데이터가 있으면 다음 주소, 이렇게 비어 있는 주소를 선형적으로 찾는다.
예를 들어 크기가 13인 나눗셈법 기반 해시 함수를 이용하는 해시 테이블이 존재한다.
여기에 42를 넣으면 42 % 13 = 3 이므로, 42는 테이블의 3번째 요소에 삽입한다.
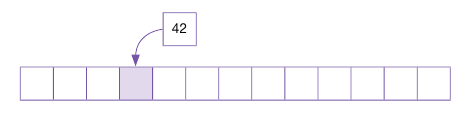
이어서 55를 다시 삽입한다.
55 % 13 = 3 이므로, 이미 사용 중인 주소로 충돌이 일어났다.
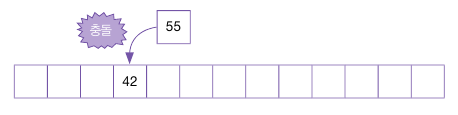
충돌이 일어났으므로, 55를 넣을 주소를 다시 찾아야 한다.
충돌이 일어난 주소에서 뒤로 1칸 이동하여 주소를 확인하면 빈 주소이므로 이 요소에 55를 삽입한다.
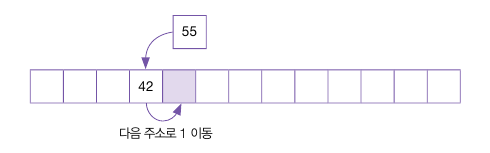
또 다시 81을 입력한다.
81 % 13 = 3 이므로, 충돌이 발생하였다.
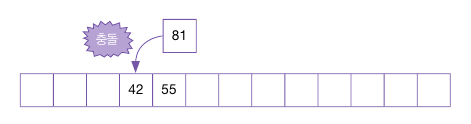
81이 들어갈 주소를 찾아야 하는데, 뒤 1칸은 55값이 들어 있으므로, 다시 1칸을 확인하여 빈 주소인지 확인한다.
빈 주소이므로 이 요소에 81을 삽입한다.
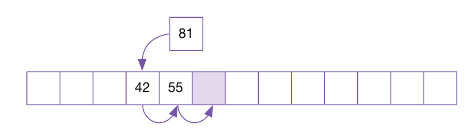
이처럼 선형 탐사는 충돌할 뻔한 데이터들이 한 곳에 모이는 클러스터(Cluster) 현상이 발생한다.
클러스터 현상이 발생하면 새로운 주소를 찾기 위해 수행하는 선형 탐사 시간이 길어지고, 이로 인해 해시 테이블의 성능은 저하된다.
그래서 선형 탐사 방법은 효율적인 알고리즘이 아니며, 이 문제를 개선한 알고리즘이 제곱 탐사 알고리즘이다.
제곱 탐사(Quadratic Probing)
제곱 탐사는 선형 탐사와 비슷하지만, 다음 주소를 탐색하는 이동폭이 제곱수로 늘어나는 탐사 방법이다.
예를 들어, 크기가 13인 해시 테이블에 키가 42인 데이터를 삽입한다.
해시 함수는 나눗셈법 기반을 사용하고 있기 때문에 42 % 13 = 3 이므로 3 요소에 삽입한다.
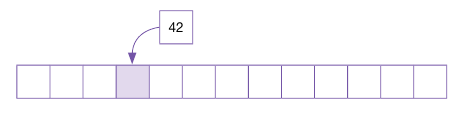
이어서 55를 입력한다.
55 % 13 = 3이므로 이미 사용 중인 주소로 데이터를 삽입할 수 없으며, 다음 주소를 탐사해야 한다.
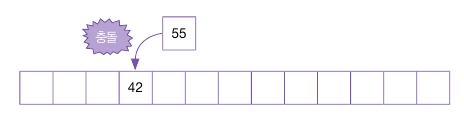
여기서 제곱 탐사를 시작하는데, 말 그대로 제곱수만큼 이동하는 방법이다.
제곱수의 시작은 1로, 1의 제곱은 1이니 1만큼만 이동한다.
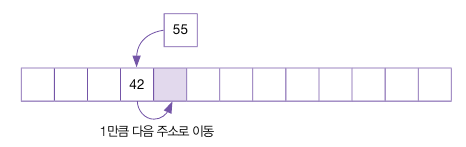
다시 81을 입력하는데, 81 % 13 = 3 이므로, 충돌이 일어난다.
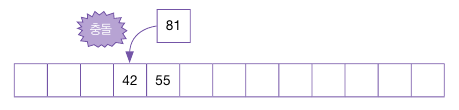
다시 제곱 탐사를 하는데, 처음 1의 제곱수(1칸) 만큼 이동하는데, 이 주소는 55 값이 사용하고 있는 주소이다.
두 번째 탐사를 시작하는데, 두 번째는 2의 제곱, 즉 4만큼 이동하여 탐사한다.
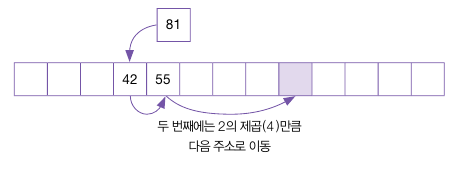
결과로 똑같은 해시 값을 가진 데이터들이 각각 해시 테이블에 입력된다.
이처럼 데이터간의 거리가 멀어져 선형 탐사와 같이 클러스터 현상이 발생하지 않는다.
하지만 이 제곱 탐사 방법에도 문제가 있는데, 다시 예를 보며 109를 삽입한다.
109 % 13은 6이므로 충돌 없이 정상적으로 삽입된다.
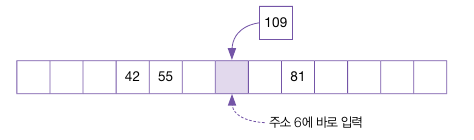
여기서 보는 문제점이, 제곱 탐사는 충돌이 일어났을 때 제곱수의 폭으로 이동한다는 규칙이 있기 때문에, 또 다른 종류의 클러스터가 발생한다.
아래 그림을 보면, 선형 탐사에 의해 발생한 클러스터와는 조금 다르지만, 엄연한 클러스터가 발생했다.
이런 현상이 발생하는 이유는 하나의 주소에서 충돌이 발생할 경우 탐사할 위치가 정해져 있기 때문이다.
제곱 탐사는 서로 다른 해시값을 가진 데이터에 대해 클러스터가 형성되지 않는 효과가 있지만, 같은 해시값을 가진 데이터에 대해서는 2차 클러스터를 형성하는 문제도 갖고 있다.
전체적으로 이러한 문제를 해결하는 방법이 바로 이중 해싱 알고리즘이다.
이중 해싱(Double Hashing)
이중 해싱 방법은 쉽게 말해 해시 함수를 2개를 준비해서 해싱하는 방법을 말한다.
하나의 해시 함수는 처음 주소를 얻을 때, 또 다른 하나는 충돌이 일어날 때 탐사 이동폭을 얻기 위해 사용한다.
예를 들어 크기가 13인 해시 테이블이 있고 해싱할 해시 함수 2가지가 있다.
// 처음 해싱할 함수
int Hash(int key)
{
return Key % 13; // 테이블 사이즈 13
}
// 충돌 시 사용하는 함수
int Hash2(int Key)
{
return (Key % 11) + 2;
}
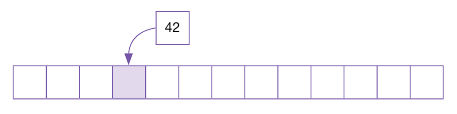
42 데이터를 삽입할 때 42 % 13 = 3 이므로, 주소 3에 정상적으로 입력이 된다.
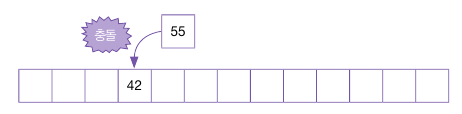
이어서 55를 삽입하는데, 55 % 13 = 3 이므로, 이미 사용 중인 주소로 충돌이 발생한다.
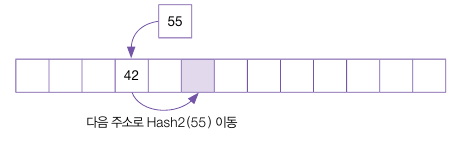
여기서 새로운 주소를 탐사하는데, Hash2() 함수를 이용해서 이동폭을 얻는다.
Hash2 함수에 55를 매개 변수로 넘기면 55 % 11 = 0 이므로, +2의 값인 2를 반환한다.
55의 새 주소는 원래의 주소(3)에 이동폭(2)을 더한 5가 되므로, 요소 5에 삽입한다.
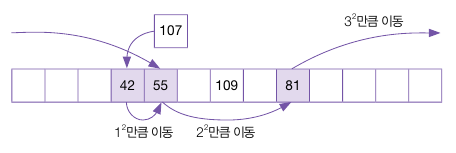
다시 81을 삽입하는데, 81 % 13 = 3이므로, 역시 충돌이 일어난다.
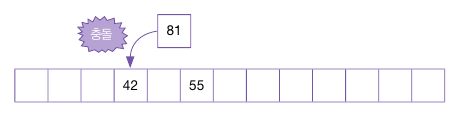
다시 81을 삽입할 주소를 찾아야 하기 때문에 Hash2() 함수로 이동폭을 계산한다.
81 % 11 = 4, +2를 하면 6으로, 3의 주소에서 6을 더하면 3 + 6 = 9가 된다.
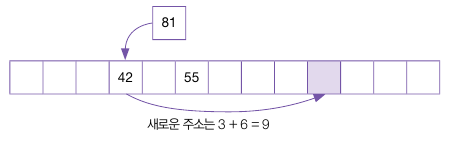
이처럼 이중 해싱을 이용하면 1, 2차 클러스터를 효과적으로 방지하여 해시 테이블의 성능 유지를 돕는다.
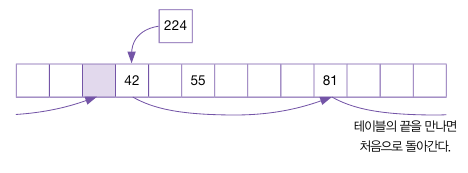
마지막으로 224를 입력하면, 첫 주소3, 다음 주소 9 다 충돌이 발생한다.
이 경우 다시 Hash2() 반환인 6만큼 이동하여 새 주소 15에 삽입한다.
하지만 테이블의 크기가 13이므로, 벗어난 경우 첫 주소부터 다시 시작하여 2의 주소에 삽입한다.
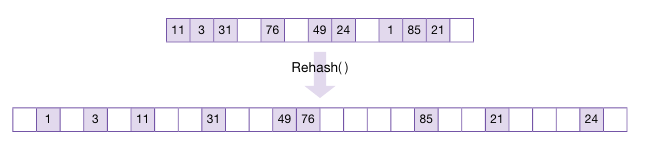
재해싱(Rehashing)
재해싱이란 해시 테이블의 크기를 늘리고, 늘어난 해시 테이블의 크기에 맞춰 테이블 내의 모든 데이터를 다시 해싱한다.
선형 탐사, 제곱 탐사, 이중 해시 등 해시 충돌 알고리즘을 적용하더라도 해시 테이블의 여유 공간이 모두 차서 발생하는 성능 저하는 막을 방법이 없다. (이 경우 연쇄 충돌 자주 발생)

그래서 재해싱 방법은 해시 테이블의 성능을 늘리는 중요한 알고리즘이다.
재해싱을 적용하면 테이블 안에 또다시 여유 공간이 생기므로 연쇄 충돌을 방지할 수 있다.
통계적으로 보면 해시 테이블의 공간 사용률이 70% ~ 80%에 이르면 성능 저하가 발생하기 시작한다.
그래서 사용률이 이까지 차기전에 미리 재해싱을 해야 성능 저하를 막을 수 있다.
그렇다고 재해싱 임계치를 낮게 잡아 계속 재해싱하면 또 성능 저하를 일으킬 수 있다.
그래서 임계치를 75%로 설정하는 것이 일반적이다.
해시 테이블 구현 함수
// 해시 테이블 생성
HashTable* CreateHashTable(int tableSize);
// 해시 테이블 소멸
void DestroyHashTable(Node* table);
// 노드 클리어
void ClearNode(Node* node);
// 이중 해싱
int Hash(char* key, int keyLength, int tableSize);
int Hash2(char* key, int keyLength, int tableSize);
// 주소 내에 데이터 확인
char* GetValue(HashTable* table, char* key);
// 데이터 삽입
void Insert(HashTable* table, char* key, char* value);
// 재해싱
void Rehashing(HashTable** table);
예제 코드
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
// 해시 테이블이 비어 있을 때 0, 비어 있지 않으면 1
enum ElementStatus
{
EMPTY = 0,
OCCUPIED = 1
};
typedef struct _Node
{
char* key;
char* value;
enum ElementStatus status;
} Node;
typedef struct _HashTable
{
int occupiedCount;
int tableSize;
Node* table;
} HashTable;
// 해시 테이블 생성
HashTable* CreateHashTable(int tableSize);
// 해시 테이블 소멸
void DestroyHashTable(HashTable* table);
// 노드 클리어
void ClearNode(Node* node);
// 이중 해싱
int Hash(char* key, int keyLength, int tableSize);
int Hash2(char* key, int keyLength, int tableSize);
// 주소 내에 데이터 확인
char* GetValue(HashTable* table, char* key);
// 데이터 삽입
void Insert(HashTable** table, char* key, char* value);
// 재해싱
void Rehash(HashTable** table);
int main()
{
HashTable* table = CreateHashTable(11);
Insert(&table, "A", "AAAAAAAA");
Insert(&table, "B", "BBBBBBBB");
Insert(&table, "C", "CCCCCCCC");
Insert(&table, "D", "DDDDDDDD");
Insert(&table, "E", "EEEEEEEE");
Insert(&table, "F", "FFFFFFFF");
Insert(&table, "G", "GGGGGGGG");
Insert(&table, "H", "HHHHHHHH");
Insert(&table, "I", "IIIIIIII");
Insert(&table, "J", "JJJJJJJJ");
Insert(&table, "K", "KKKKKKKK");
printf("\n");
printf("Key : [%s], Value : [%s]\n", "A", GetValue(table, "A"));
printf("Key : [%s], Value : [%s]\n", "B", GetValue(table, "B"));
printf("Key : [%s], Value : [%s]\n", "C", GetValue(table, "C"));
printf("Key : [%s], Value : [%s]\n", "D", GetValue(table, "D"));
printf("Key : [%s], Value : [%s]\n", "E", GetValue(table, "E"));
printf("Key : [%s], Value : [%s]\n", "F", GetValue(table, "F"));
printf("Key : [%s], Value : [%s]\n", "G", GetValue(table, "G"));
printf("Key : [%s], Value : [%s]\n", "H", GetValue(table, "H"));
printf("Key : [%s], Value : [%s]\n", "I", GetValue(table, "I"));
printf("Key : [%s], Value : [%s]\n", "J", GetValue(table, "J"));
printf("Key : [%s], Value : [%s]\n", "K", GetValue(table, "K"));
return 0;
}
HashTable* CreateHashTable(int tableSize)
{
// 테이블 생성
HashTable* table = (HashTable*)malloc(sizeof(HashTable));
table->table = (Node*)malloc(sizeof(Node) * tableSize);
memset(table->table, 0, sizeof(Node) * tableSize);
table->tableSize = tableSize;
table->occupiedCount = 0;
return table;
}
void DestroyHashTable(HashTable* table)
{
int i = 0;
// 링크드 리스트 제거
for(i = 0; i < table->tableSize; i++) {
ClearNode(&(table->table[i]));
}
// 해시 테이블 제거
free(table->table);
free(table);
}
void ClearNode(Node* node)
{
if(node->status == EMPTY) {
return;
}
free(node->key);
free(node->value);
}
int Hash(char* key, int keyLength, int tableSize)
{
int i = 0;
int value = 0;
for(i = 0; i < keyLength; i++) {
value = (value << 3) + key[i];
}
value = value % tableSize;
return value;
}
int Hash2(char* key, int keyLength, int tableSize)
{
int i = 0;
int value = 0;
for(i = 0; i < keyLength; i++) {
value = (value << 2) + key[i];
}
value = value % (tableSize - 3);
return value + 1;
}
char* GetValue(HashTable* table, char* key)
{
int keyLength = strlen(key);
int address = Hash(key, keyLength, table->tableSize);
int stepSize = Hash2(key, keyLength, table->tableSize);
while(table->table[address].status != EMPTY && strcmp(table->table[address].key, key) != 0) {
address = (address + stepSize) & table->tableSize;
}
return table->table[address].value;
}
void Insert(HashTable** table, char* key, char* value)
{
// keyLength : key길이, adress : 해싱한 주소, stepSize : 이동폭
int keyLength, address, stepSize;
// 재해싱 여부
double usage;
usage = (double)(*table)->occupiedCount / (*table)->tableSize;
if(usage > 0.5) {
Rehash(table);
}
keyLength = strlen(key);
address = Hash(key, keyLength, (*table)->tableSize);
stepSize = Hash2(key, keyLength, (*table)->tableSize);
while((*table)->table[address].status != EMPTY && strcmp((*table)->table[address].key, key) != 0) {
printf("Collision Occured Key : [%s], Address : [%d], StepSize : [%d]\n", key, address, stepSize);
// 데이터를 삽입할 주소 재탐색
address = (address + stepSize) % (*table)->tableSize;
}
(*table)->table[address].key = (char*)malloc(sizeof(char) * (keyLength) + 1);
strcpy((*table)->table[address].key, key);
(*table)->table[address].value = (char*)malloc(sizeof(char) * (strlen(value) + 1));
strcpy((*table)->table[address].value, value);
(*table)->table[address].status = OCCUPIED;
(*table)->occupiedCount++;
printf("Key[%s] enter at address : [%d]\n", key, address);
}
void Rehash(HashTable** table)
{
int i = 0;
Node* oldTable = (*table)->table;
// 새로운 테이블 생성
HashTable* newTable = CreateHashTable((*table)->tableSize * 2);
printf("\n Rehash. New Table Size is : %d\n\n", newTable->tableSize);
// 이전의 해시 테이블 데이터를 새 해시 테이블 데이트로 이동
for(i = 0; i < (*table)->tableSize; i++) {
if(oldTable[i].status == OCCUPIED) {
Insert(&newTable, oldTable[i].key, oldTable[i].value);
}
}
// 이전의 해시 테이블 소멸
DestroyHashTable((*table));
// 기존 테이블에 새로운 해시 테이블 주소 대입
(*table) = newTable;
}
실행 결과
Key[A] enter at address : [10]
Key[B] enter at address : [0]
Key[C] enter at address : [1]
Key[D] enter at address : [2]
Key[E] enter at address : [3]
Key[F] enter at address : [4]
Rehash. New Table Size is : 22
Key[B] enter at address : [0]
Key[C] enter at address : [1]
Key[D] enter at address : [2]
Key[E] enter at address : [3]
Key[F] enter at address : [4]
Key[A] enter at address : [21]
Key[G] enter at address : [5]
Key[H] enter at address : [6]
Key[I] enter at address : [7]
Key[J] enter at address : [8]
Key[K] enter at address : [9]
Key : [A], Value : [AAAAAAAA]
Key : [B], Value : [BBBBBBBB]
Key : [C], Value : [CCCCCCCC]
Key : [D], Value : [DDDDDDDD]
Key : [E], Value : [EEEEEEEE]
Key : [F], Value : [FFFFFFFF]
Key : [G], Value : [GGGGGGGG]
Key : [H], Value : [HHHHHHHH]
Key : [I], Value : [IIIIIIII]
Key : [J], Value : [JJJJJJJJ]
Key : [K], Value : [KKKKKKKK]
출처 : 이것이 자료구조+알고리즘이다 with C언어
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] C - 우선순위 큐(Priority Queue) (0) | 2022.12.10 |
|---|---|
| [Algorithm] C - 수식 트리(Expression Tree) (1) | 2022.12.04 |
| [Algorithm] C - 이진 트리(Binary Tree) (0) | 2022.12.04 |
| [Algorithm] C - 트리(Tree) 자료 구조 (0) | 2022.12.04 |
| [Algorithm] C - 이진 탐색 트리(Binary Search Tree) (4) | 2022.12.03 |