먼저 아래와 같은 큐 구조가 있다.
유선순위 큐의 각 요소는 우선순위를 가지고, 이들 요소의 우선순위 오름차순으로 연결된다.
이 예제에서는 낮은 값의 데이터들이 높은 우선순위를 가진다.

위 큐에서 20의 값을 넣는 과정을 살펴보면, 먼저 첫 요소부터 순서차적으로 우선순위를 비교한다.
20은 2와 17보다 크고 22보다 작으므로 17과 22사이에 삽입되어야 한다.

우선순위 큐의 제거
우선순위 큐의 제거 연산은 가장 앞 요소인 전단만 제거하면 되므로, 간단하다.

힙을 이용한 우선순위 큐 구현 방법
우선순위 큐를 구현하기 위해 힙을 이용한다.
여기서 힙(Heap)은 자유 저장소의 힙이 아닌, 힙 순서 속성(Heap Order Priority)을 만족하는 완전 이진트리를 말한다.
완전 이진 트리란 최고 깊이(잎 노드) 노드들을 제외한 나머지 노드들이 모두 채워져 있는 이진 트리를 말한다.
아래 트리의 구조가 완전 이진 트리 구조이며, 최고 깊이 노드들이 모두 채워져 있지 않은 것을 볼 수 있다.

여기서 중요한 부분은 힙 순서 속성이며, 이 속성을 이해해야 우선순위 큐를 구현할 수 있다.
힙 순서 속성이란 쉽게 말해 트리 내의 모든 노드가 부모 노드보다 커야한다 라는 규칙이다.
여기서 뿌리 노드는 맨 위 루트 노드이니 제외한다.
아래 트리 구조가 힙 순서를 만족하는 이진트리로, 힙의 예이다.
노드 값을 보면 깊이가 깊어질 수록 값이 더 커지는 것을 볼 수 있다.

힙의 가장 중요한 점은 힙에서 가장 작은 데이터를 갖는 노드는 뿌리 노드라는 점이다.
이 점에 따라 힙에 사용되는 연산은 2가지 뿐이며, 하나는 새 노드를 삽입하는 연산, 그리고 뿌리노드를 없애는 최솟값 삭제 연산이다.
힙의 삽입 연산
힙의 삽입 연산은 3단계를 거쳐 이루어진다.
- 힙의 최고 깊이 가장 우측에 새 노드를 추가한다. 이때 힙은 완전 이진 트리를 유지하여야 한다.
- 삽입한 노드를 부모 노드와 비교하여 삽입한 노드가 부모 노드보다 크면 제 위치에 삽입된 것으로 종료한다.
(만약 이때 반대로 부모 노드보다 작을 경우 다음 단계를 진행한다.) - 삽입한 노드가 부모 노드보다 작으면 부모 노드와 삽입한 위치를 서로 바꾸고, 다시 2번의 단계로 돌아가 진행한다.
삽입 연산은 새로 삽입한 노드가 힙 순서 속성을 만족할 때까지 그 노드를 부모 노드와 교환하는 것이 핵심이다.
힙 노드 삽입 예제
아래와 같은 힙이 있으며, 이 힙에 7을 삽입하는 예제이다.
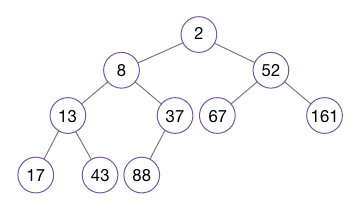
새 노드 7을 힙의 가장 깊은 곳에 추가한다.
이때 완전 이진트리가 깨지면 안되므로, 노드 37의 오른쪽 자식에 추가한다.
그리고 추가한 노드(7)와 부모 노드(37)을 비교한다.
7은 37보다 작으므로 새로 추가한 노드와 부모 노드 자리를 교환(3번 과정)한다.

7이 37과 교환되어 한 단계 올라갔으며, 다시 부모 노드와 비교한다.
추가한 노드(7)와 부모 노드(8)간 비교 시 추가한 노드가 값이 작으므로 다시 교환을 수행한다.

다시 7이 한 단계 올라왔고, 비교할 노드가 뿌리 노드밖에 남지 않았다.
뿌리 노드(2)는 7보다 작으므로 힙 순서 속성을 위반하지 않는다.
이것으로 삽입 연산이 완성된 것이다.
힙 최솟값 노드 삭제 연산
힙에서의 최솟값 삭제는 곧 뿌리 노드를 삭제한다는 말과 같은 의미이다.
힙 구조에서는 뿌리 노드의 삭제는 큰 문제가 아니며 삭제 후 힙 순서 속성을 유지하는 것이 문제이다.
예를 들어, 아래와 같은 구조에서 뿌리 노드를 삭제하고, 힙 순서 속성을 유지하는 과정이다.

- 힙의 최고 깊이 가장 우측에 있던 노드를 뿌리 노드로 옮김
(이때 힙 순서 속성 파괴) - 옮겨온 노드의 양쪽 자식을 비교하여 작은쪽 자식과 위치 교환
(힙 순서 속성을 지키려면 부모 노드는 양쪽 자식보다 작은 값을 가져야 함) - 옮겨온 노드가 더 이상 자식이 없는 잎 노드로 되거나 양쪽 자식보다 작은 값을 갖는 경우 삭제 연산 종료
(그렇지 않은 경우 2번 재 반복)
아래 과정은 위 과정을 상세 과정으로 설명하는 내용이다.
먼저 힙에서 최솟값 노드(뿌리)를 삭제한다.

힙의 최고깊이 가장 우측 노드를 삭제된 뿌리 노드가 있던 곳으로 옮긴다.
그 후 힙 순서 속성의 위반 여부를 살펴야 한다.
힙 순서 속성에 의하면 부모 노드 값 < 자식 노드 값을 가져야 하는데, 뿌리 노드(37)이 왼쪽 자식 노드(7)보다 크므로 힙 순서 속성을 위반한다.
그래서 뿌리 노드는 양쪽 자식 중 작은 값을 가진 노드와 교환한다. (왼쪽 자식 노드 <-> 뿌리 노드)

뿌리 노드와 왼쪽 자식 노드의 값 교환으로 인해 37이 한 단계 내려온 것을 볼 수 있다.
다시 힙 순서 속성의 위반 여부를 확인한다.
37이 양쪽 자식(13, 8) 보다 크므로 더 작은 값인 오른쪽 자식 노드(8)와 서로 노드를 교환한다.

다시 37이 한 단계 내려왔으며, 또 다시 힙 순서 속성 위반 여부를 확인한다.
37 노드의 자식 노드의 값을 확인 하였더니 88로, 더 이상 힙 순서 속성을 위반하지 않는다.
이것으로 삭제 연산이 완료된 것이다.

예제 코드
#include <stdio.h>
#include <stdlib.h>
#include <memory.h>
typedef struct _Node
{
int priority; // 출력해야할 우선순위
void* data; // 노드 값
} Node;
typedef struct _PriorityQueue
{
Node* node; // 데이터를 담을 노드
int capacity; // node의 크기
int usedSize; // node 안에 들어있는 큐 요소의 수
} PriorityQueue;
PriorityQueue* CreateQueue(int size);
void DestroyQueue(PriorityQueue* pq);
void Enqueue(PriorityQueue* pq, Node newNode);
void Dequeue(PriorityQueue* pq, Node* root);
int GetParent(int index);
int GetLeftChild(int index);
void SwapNodes(PriorityQueue* pq, int aIndex, int bIndex);
int IsEmpty(PriorityQueue* pq);
void PrintNode(Node* node);
int main()
{
PriorityQueue* pq = CreateQueue(3);
Node popped;
Node nodes[7] = {
{34, (void*)"코딩"},
{12, (void*)"밥먹기"},
{87, (void*)"커피타기"},
{45, (void*)"문서작성"},
{35, (void*)"디버깅"},
{66, (void*)"이닦기"},
};
Enqueue(pq, nodes[0]);
Enqueue(pq, nodes[1]);
Enqueue(pq, nodes[2]);
Enqueue(pq, nodes[3]);
Enqueue(pq, nodes[4]);
Enqueue(pq, nodes[5]);
printf("큐에 남아 있는 작업의 수 : %d\n", pq->usedSize);
while(!IsEmpty(pq)) {
Dequeue(pq, &popped);
PrintNode(&popped);
}
return 0;
}
PriorityQueue* CreateQueue(int size)
{
PriorityQueue* newQueue = (PriorityQueue*)malloc(sizeof(PriorityQueue));
newQueue->capacity = size;
newQueue->usedSize = 0;
newQueue->node = (Node*)malloc(sizeof(Node) * newQueue->capacity);
return newQueue;
}
void DestroyQueue(PriorityQueue* pq)
{
free(pq->node);
free(pq);
}
void Enqueue(PriorityQueue* pq, Node newNode)
{
int currentPosition = pq->usedSize;
int parentPosition = GetParent(currentPosition);
if(pq->usedSize == pq->capacity) {
if(pq->capacity == 0) {
pq->capacity = 1;
}
pq->capacity *= 2;
pq->node = (Node*)realloc(pq->node, sizeof(Node) * pq->capacity);
}
pq->node[currentPosition] = newNode;
// 후속 처리
while(currentPosition > 0 && pq->node[currentPosition].priority < pq->node[parentPosition].priority) {
SwapNodes(pq, currentPosition, parentPosition);
currentPosition = parentPosition;
parentPosition = GetParent(currentPosition);
}
pq->usedSize++;
}
void Dequeue(PriorityQueue* pq, Node* root)
{
int parentPosition = 0;
int leftPosition = 0;
int rightPosition = 0;
memcpy(root, &pq->node[0], sizeof(Node));
memset(&pq->node[0], 0, sizeof(Node));
pq->usedSize--;
SwapNodes(pq, 0, pq->usedSize);
leftPosition = GetLeftChild(0);
rightPosition = leftPosition + 1;
while(1) {
int selectChild = 0;
if(leftPosition >= pq->usedSize) {
break;
}
if(rightPosition >= pq->usedSize) {
selectChild = leftPosition;
}
else {
if(pq->node[leftPosition].priority > pq->node[rightPosition].priority) {
selectChild = rightPosition;
}
else {
selectChild = leftPosition;
}
}
if(pq->node[selectChild].priority < pq->node[parentPosition].priority) {
SwapNodes(pq, parentPosition, selectChild);
parentPosition = selectChild;
}
else {
break;
}
leftPosition = GetLeftChild(parentPosition);
rightPosition = leftPosition + 1;
}
if(pq->usedSize < (pq->capacity / 2)) {
pq->capacity /= 2;
pq->node = (Node*)realloc(pq->node, sizeof(Node) * pq->capacity);
}
}
int GetParent(int index)
{
return (int) ((index - 1) / 2);
}
int GetLeftChild (int index)
{
return (2 * index) + 1;
}
void SwapNodes(PriorityQueue* pq, int aIndex, int bIndex)
{
int copySize = sizeof(Node);
Node* temp = (Node*)malloc(copySize);
memcpy(temp, &pq->node[aIndex], copySize);
memcpy(&pq->node[aIndex], &pq->node[bIndex], copySize);
memcpy(&pq->node[bIndex], temp, copySize);
free(temp);
}
int IsEmpty(PriorityQueue* pq)
{
return (pq->usedSize == 0);
}
void PrintNode(Node* node)
{
printf("작업명 : %s (우선순위 : %d)\n", node->data, node->priority);
}
실행 결과
큐에 남아 있는 작업의 수 : 6
작업명 : 밥먹기 (우선순위 : 12)
작업명 : 코딩 (우선순위 : 34)
작업명 : 디버깅 (우선순위 : 35)
작업명 : 문서작성 (우선순위 : 45)
작업명 : 이닦기 (우선순위 : 66)
작업명 : 커피타기 (우선순위 : 87)
출처 : 이것이 자료구조+알고리즘이다 with C언어
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] C - 해시 테이블(Hash Table) (0) | 2022.12.12 |
|---|---|
| [Algorithm] C - 수식 트리(Expression Tree) (1) | 2022.12.04 |
| [Algorithm] C - 이진 트리(Binary Tree) (0) | 2022.12.04 |
| [Algorithm] C - 트리(Tree) 자료 구조 (0) | 2022.12.04 |
| [Algorithm] C - 이진 탐색 트리(Binary Search Tree) (4) | 2022.12.03 |