[Algorithm] C - 링크드 리스트(Linked List)

Algorithm/이론

[Algorithm] C - 링크드 리스트(Linked List)

유제필 2022. 11. 6. 15:30

요약

배열의 반대 개념으로, 데이터의 크기를 유연하게 변경할 수 있음
첫 데이터를 헤드, 끝 데이터를 테일, 각 데이터를 노드라고 부름
다음 노드의 주소를 이전 노드의 저장하여 다음 노드의 주소로 접근
데이터의 접근이 어려우나, 생성, 소멸, 삭제 등은 쉬움

장점

새로운 노두의 추가, 삽입, 삭제가 쉽고 빠름. (배열은 새로운 요소를 삽입하거나 삭제를 하기 어려움)
현재 노드의 다음 노드를 얻어오는 연산에 대해 비용이 발생하지 않음

단점

다음 노드를 가리키려는 포인터 때문에 각 노드마다 추가적인 메모리가 필요함
특정 위치에 있는 노드에 접근하기 위한 비용이 크며 접근하기 까지 시간이 많이 필요함 (노드에 접근하기 위해 N - 1회의 접근이 필요함)

리스트란

리스트는 이름과 같이 목록 형태로 이루어진 데이터 형식을 말한다.
리스트의 목록을 이루는 개별 요소를 노드(node)라고 한다.

리스트의 첫 번째 노드를 헤드(Head), 마지막 노드를 테일(Tail)이라고 부르며 리스트의 길이는 헤드부터 테일까지의 노드 수이다.

리스트와 비슷한 데이터 형식으로 배열이 존재한다.
배열과 리스트의 차이는 배열은 생성 시 배열의 크기를 지정해 주어야 한다.(정적)
반면 리스트는 배열과 반대로 유연하게 크기를 바꿀 수 있다.(동적)

리스트의 구조는 링크드 리스트, 더블 링크드 리스트, 환형 링크드 리스트 등이 있다.

링크드 리스트(Linked List)

링크드 리스트란 노드를 연결해서 만든 리스트라고 한다.
링크드 리스트의 노드는 데이터를 보관하는 필드, 다음 노드와 연결 고리 역할을 하는 포인터로 이루어진다.

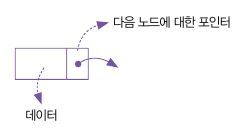
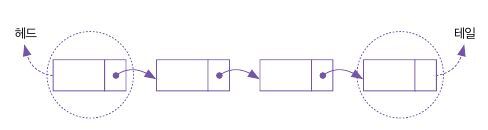
링크드 리스트는 포인터만 교환하면 노드 사이에 노드를 끼워 넣거나 제거하는 부분이 간단하게 이루어진다.
C언어에서 링크드 리스트는 다음과 같은 구조체로 나타낸다.

typedef int ElementType;

// 노드 구조체 정의
typedef struct tagNode
{
    ElementType data;
    struct tagNode* nextNode;
} Node;

링크드 리스트의 주요 연산

링크드 리스트의 주요 연산은 두 종류로, 자료구조를 구축하기 위한 연산과 자료구조에 저장된 데이터를 활용하기 위한 연산이다

노드 생성(CreatedNode) 및 소멸(DestroyNode)
노드 추가(AppendNode)
노드 탐색(GetNodeAt)
노드 삭제(RemoveNode)
노드 삽입(InsertAfter, InsertNewHead)

위 리스트 중 생성 및 소멸, 추가 삭제는 자료구조를 구축하기 위한 연산, 탐색은 활용 연산이다.

노드의 생성/소멸 연산

노드를 생성하기 위해 힙 메모리 영역에 데이터를 할당해야 한다.
지역 변수로 같이 데이터를 생성하면 함수가 종료되면서 스택에 있던 데이터는 소멸된다.

// 노드 생성
Node* SLL_CreateNode(ElementType newData)
{
    Node* newNode = (Node*)malloc(sizeof(Node));
    
    
    newNode->data = newData;    // 데이터 저장
    newNode->nextNode = NULL;   // 다음 노드에 대한 포인터 NULL로 초기화
    
    return newNode;     // 노드 주소 반환
}

노드의 소멸시키는 방법은 free 함수로 간단하게 처리할 수 있다.

// 노드 소멸
void SLL_DestroyNode(Node* node)
{
    free(node);
}

노드 추가 연산

노드 추가는 링크드 리스트의 테일 노드 뒤에 새로운 노드를 만들어 연결하는 연산이다.

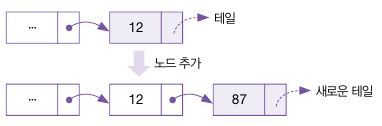
SLL_CreateNode() 함수를 이용하여 힙 메모리에 노드 생성 후 생성한 노드의 주소를 테일의 NextNode 포인터에 저장한다.

// 노드 추가
void SLL_AppendNode(Node** head, Node* newNode)
{
    // 헤드 노드가 NULL일 경우 새로운 헤드 생성
    if((*head) == NULL) {
        *head = newNode;
    }
    else {
        // 헤드가 존재할 경우 테일을 찾아 NewNode를 연결
        Node* tail = (*head);
        while(tail->nextNode != NULL) {
            tail = tail->nextNode;
        }
        
        tail->nextNode = newNode;
    }
}

노드 탐색 연산

링크드 리스트에서 노드에 접근하기 위해서는 헤드부터 다음 노드에 대한 포인터를 징검다리 삼아 모든 노드를 거쳐야 한다.
찾고자 하는 요소가 N번째에 있다면 N - 1개의 노드를 전부 거쳐야 하므로 비효울적이다.
이 경우가 링크드 리스트의 단점이며, 반대로 정적인 배열은 한 번에 거칠수 있으므로 반대의 개념이 된다.

// 노드 탐색
Node* SLL_GetNodeAt(Node* head, int location)
{
    Node* current = head;
    
    // 다음 노드 주소 탐색
    while(current != NULL && (--location) >= 0) {
        current = current->nextNode;
    }
    
    return current;
}

노드 삭제 연산

노드 삭제의 경우 삭제하고자 하는 노드를 찾고 다음 노드를 이전 노드의 NextNode 포인터에 연결하면 된다.

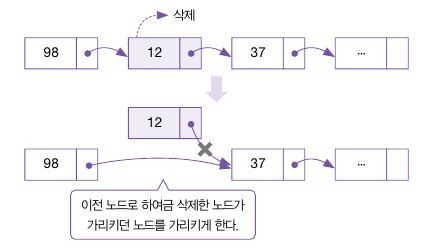
// 노드 제거
void SLL_RemoveNode(Node** head, Node* removeNode)
{
    if(*head == removeNode)
    {
        *head = removeNode->nextNode;
    }
    else {
        Node* current = *head;
        while(current != NULL && current->nextNode != removeNode) {
            current = current->nextNode;
        }
        
        if(current != NULL) {
            current->nextNode = removeNode->nextNode;
        }
    }
}

노드 삽입

노드 삽입은 노드와 노드 사이에 새로운 노드를 끼워 넣는 연산이다.

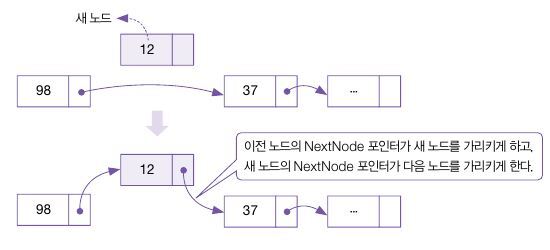
// 노드 삽입
void SLL_InsertAfter(Node* current, Node* newNode)
{
    newNode->nextNode = current->nextNode;
    current->nextNode = newNode;
}

// 헤드 삽입
void SLL_InsertNewHead(Node** head, Node* newHead)
{
    if(head == NULL) {
        (*head) = newHead;
    }
    else {
        newHead->nextNode = (*head);
        (*head) = newHead;
    }
}

노드 개수 세기

노드의 개수를 세는 연산은 링크드 리스트 내에 존재하는 모든 노드의 개수를 반환한다.

// 노드 개수
int SLL_GetNodeCount(Node* head)
{
    int count = 0;
    Node* current = head;
    
    // 다음 노드가 NULL이 아닐 경우 카운트 1씩 증가
    while(current != NULL) {
        current = current->nextNode;
        count++;
    }
    
    return count;
}

예제 코드

#include <stdio.h>
#include <stdlib.h>

typedef int ElementType;

// 노드 구조체 정의
typedef struct tagNode
{
    ElementType data;
    struct tagNode* nextNode;
} Node;

// 함수 원형
Node* SLL_CreateNode(ElementType NewData);          // 노드 생성
void SLL_DestroyNode(Node* Node);                   // 노드 소멸
void SLL_AppendNode(Node** Head, Node* NewHead);    // 노드 추가
void SLL_InsertAfter(Node* Current, Node* NewNode); // 노드 삽입
void SLL_InsertNewHead(Node** Head, Node* NewHead); // 헤드 삽입
void SLL_RemoveNode(Node** Head, Node* Remove);     // 노드 삭제
Node* SLL_GetNodeAt(Node* Head, int Location);      // 노드 탐색
int SLL_GetNodeCount(Node* Head);                   // 노드 개수

int main()
{
    int i = 0;
    int count = 0;
    Node* list = NULL;
    Node* current = NULL;
    Node* newNode = NULL;
    
    for(i = 0; i < 5; i++) {
        newNode = SLL_CreateNode(i);
        SLL_AppendNode(&list, newNode);
    }
    
    newNode = SLL_CreateNode(-1);
    SLL_InsertNewHead(&list, newNode);
    
    newNode = SLL_CreateNode(-2);
    SLL_InsertNewHead(&list, newNode);
    
    // 노드 리스트 출력
    count = SLL_GetNodeCount(list);
    for(i = 0; i < count; i++) {
        current = SLL_GetNodeAt(list, i);
        printf("List : [%d] : %d\n", i, current->data);
    }
    
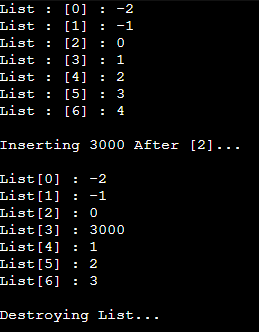
    // 리스트의 세 번째 노드 뒤에 새 노드 삽입
    printf("\nInserting 3000 After [2]...\n\n");
    
    current = SLL_GetNodeAt(list, 2);
    newNode = SLL_CreateNode(3000);
    
    SLL_InsertAfter(current, newNode);
    
    // 노드 리스트 출력
    for(i = 0; i < count; i++) {
        current = SLL_GetNodeAt(list ,i);
        printf("List[%d] : %d\n", i, current->data);
    }
    
    // 모든 노드 소멸
    printf("\nDestroying List...\n");
    
    for(i = 0; i < count; i++) {
        current = SLL_GetNodeAt(list ,0);
        
        if(current != NULL) {
            SLL_RemoveNode(&list, current);
            SLL_DestroyNode(current);
        }
    }
    
    return 0;
}

// 노드 생성
Node* SLL_CreateNode(ElementType newData)
{
    Node* newNode = (Node*)malloc(sizeof(Node));
    
    
    newNode->data = newData;    // 데이터 저장
    newNode->nextNode = NULL;   // 다음 노드에 대한 포인터 NULL로 초기화
    
    return newNode;     // 노드 주소 반환
}

// 노드 소멸
void SLL_DestroyNode(Node* node)
{
    free(node);
}

// 노드 추가
void SLL_AppendNode(Node** head, Node* newNode)
{
    // 헤드 노드가 NULL일 경우 새로운 헤드 생성
    if((*head) == NULL) {
        *head = newNode;
    }
    else {
        // 헤드가 존재할 경우 테일을 찾아 NewNode를 연결
        Node* tail = (*head);
        while(tail->nextNode != NULL) {
            tail = tail->nextNode;
        }
        
        tail->nextNode = newNode;
    }
}

// 노드 삽입
void SLL_InsertAfter(Node* current, Node* newNode)
{
    newNode->nextNode = current->nextNode;
    current->nextNode = newNode;
}

// 헤드 삽입
void SLL_InsertNewHead(Node** head, Node* newHead)
{
    if(head == NULL) {
        (*head) = newHead;
    }
    else {
        newHead->nextNode = (*head);
        (*head) = newHead;
    }
}

// 노드 제거
void SLL_RemoveNode(Node** head, Node* removeNode)
{
    if(*head == removeNode)
    {
        *head = removeNode->nextNode;
    }
    else {
        Node* current = *head;
        while(current != NULL && current->nextNode != removeNode) {
            current = current->nextNode;
        }
        
        if(current != NULL) {
            current->nextNode = removeNode->nextNode;
        }
    }
}

// 노드 탐색
Node* SLL_GetNodeAt(Node* head, int location)
{
    Node* current = head;
    
    // 다음 노드 주소 탐색
    while(current != NULL && (--location) >= 0) {
        current = current->nextNode;
    }
    
    return current;
}

// 노드 개수
int SLL_GetNodeCount(Node* head)
{
    int count = 0;
    Node* current = head;
    
    // 다음 노드가 NULL이 아닐 경우 카운트 1씩 증가
    while(current != NULL) {
        current = current->nextNode;
        count++;
    }
    
    return count;
}

실행 결과

https://github.com/JeHeeYu/Algorithm/blob/main/List/Single%20Linked%20List/LinkedList.c

GitHub - JeHeeYu/Algorithm: 알고리즘 문제 풀이

알고리즘 문제 풀이. Contribute to JeHeeYu/Algorithm development by creating an account on GitHub.

github.com

출처 : 이것이 자료구조+알고리즘이다 with c 언어

'Algorithm > 이론' 카테고리의 다른 글

[Algorithm] C - 재귀함수(Recursion) (2)	2022.11.12
[Algorithm] C - 큐(Queue) (0)	2022.11.08
[Algorithm] C - 스택(Stack) (0)	2022.11.07
[Algorithm] C - 환형 더블 링크드 리스트(Circular Double Linked List) (0)	2022.11.07
[Algorithm] C - 더블 링크드 리스트(Double Linked List) (0)	2022.11.06

현재글[Algorithm] C - 링크드 리스트(Linked List)

임베디드 개발자 유제필의 블로그 입니다.

arm, 알고리즘, Flutter, Mat 클래스, Computer Vision, 백준, Embedded, 자료구조, 문자열 검색, OpenCV, C, 임베디드, 트리, C언어, c++, DART, STM32, Baekjoon, Linux, 정렬,

Today :
Yesterday :

일	월	화	수	목	금	토
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

유제필의 개발 블로그