요약
링 버퍼 큐 복잡도 : O(1)
배열 큐 복잡도 : O(n)
- 가장 먼저 넣은 데이터를 가장 먼저 꺼내는 선입선출 구조인 FIFO(First In - First Out) 구조를 따름
- 큐에 데이터를 넣는 작업을 인큐(Enqueue), 또는 스택과 같이 푸쉬(Push)라고 함
- 큐에서 데이터를 꺼내는 작업을 디큐(Dequeue) 또는 스택과 같이 팝(Pop)이라고 함
- 데이터를 꺼내는 쪽을 프론트(Front), 데이터를 넣는 쪽을 리어(Rear)라고 함
- 링 버퍼는 배열의 처음과 끝이 연결되어 있는 구조로, 배열 요소를 앞쪽으로 옮기지 않아도 되어 좀 더 효율적인 구조로 사용 가능
- 일반 배열로 사용하는 큐로 구현 시 배열 요소를 앞쪽으로 옮겨야 하는 작업이 필요
큐(Queue)란
큐란 스택과 비슷한 자료구조로, 데이터를 일시적으로 쌓아 놓고 사용하는 자료구조의 일종이다.
큐는 가장 먼저 넣은 데이터를 가장 먼저 꺼내는 선입선출 구조인 FIFO(First In - First Out) 구조를 따른다.
예를 들어, 은행 창구에서 차례를 기다리는 대기열이나 마트에서 계산을 기다리는 대기열을 들 수 있다.
큐에 데이터를 넣는 작업을 인큐(Enqueue), 또는 스택과 같이 푸쉬(Push)라 하고,
큐에서 데이터를 꺼내는 작업을 디큐(Dequeue) 또는 스택과 같이 팝(Pop)이라고 표현한다.
그리고 데이터를 꺼내는 쪽을 프론트(Front), 데이터를 넣는 쪽을 리어(Rear)라고 한다.

이 글에서는 일반 배열만 사용해서 만드는 큐가 아닌, 링 버퍼 큐에 관한 예제이다.
링 버퍼는 배열의 처음과 끝이 연결되어 있는 구조로, 배열 요소를 앞쪽으로 옮기지 않아도 되어
좀 더 효율적인 구조로 사용할 수 있다.
링 버퍼 큐에서는 프론트가 맨 처음 요소의 인덱스를 가리키고, 리어가 맨 끝 요소의 하나 뒤의 인덱스를 가리킨다.
(저장할 위치 미리 선정)

인큐와 디큐 과정
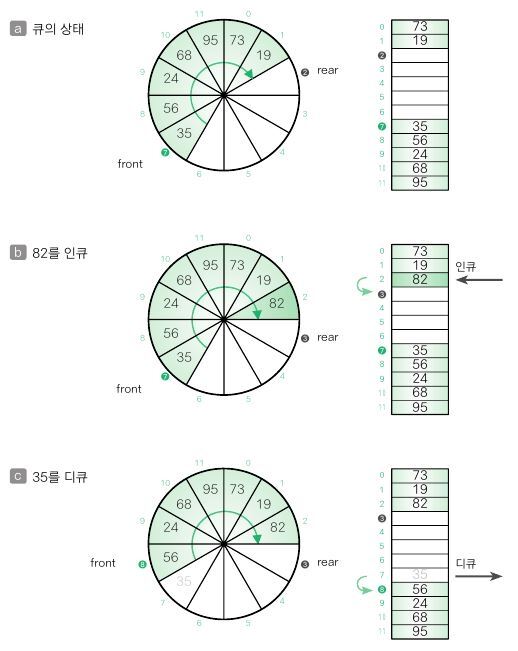
인큐와 디큐를 거치면 포론트와 리어가 아래와 같은 과정을 거치게 된다.
- 7개의 데이터(35, 56, 24, 68, 95, 73, 19)가 차례데로 que[7], que[8] ... que[11], que[0], que[1]에 저장된다.
여기서 프론트 값은 7, 리어 값은 2이다. - 82를 인큐하고, que[2]에 82를 저장한 다음, 리어 값을 1 증가시킨다.
- 35를 디큐하고, 프론트 요소의 값 35를 빼고 프론트 값을 1 증가시킨다.
큐의 구조체
일반 배열로 구성한 큐의 경우 3가지의 정보만 있으면 되지만, 링 버퍼 큐에서는 5가지의 필수 정보가 필요하다.
- 큐 최대 용량
- 큐 현재 요소 개수
- 프론트
- 리어
- 큐의 맨 앞 요소에 대한 위치
typedef struct {
int max; // 큐의 최대 용량
int num; // 현재 요소 개수
int front; // 프론트, 데이터를 꺼내는 방향
int rear; // 리어, 데이터를 넣는 방향
int *que; // 큐의 맨 앞 요소에 대한 위치
} Queue;
큐에서 사용하는 함수
int Create(Queue *q, int max); // 큐 메모리 생성
int Enque(Queue *q, int x); // 큐에 데이터 인큐
int Deque(Queue *q, int *x); // 큐에서 데이터 디큐
int Peek(const Queue *q, int *x); // 맨 앞 데이터 확인
void Clear(Queue *q); // 모든 데이터 삭제
int Capacity(const Queue *q); // 큐 최대 용량 확인
int Size(const Queue *q); // 큐에 저장된 데이터 개수
int IsEmpty(const Queue *q); // 큐가 비어 있는지 확인
int IsFull(const Queue *q); // 큐가 가득 찼는지 확인
int Search(const Queue *q, int x); // 큐에서 데이터 검색
void Print(const Queue *q); // 큐 데이터 출력
void Terminate(Queue *q); // 큐 메모리 소멸
예제 코드
#include <stdio.h>
#include <stdlib.h>
typedef struct {
int max; // 큐의 최대 용량
int num; // 현재 요소 개수
int front; // 프론트, 데이터를 꺼내는 방향
int rear; // 리어, 데이터를 넣는 방향
int *que; // 큐의 맨 앞 요소에 대한 위치
} Queue;
int Create(Queue *q, int max); // 큐 메모리 생성
int Enque(Queue *q, int x); // 큐에 데이터 인큐
int Deque(Queue *q, int *x); // 큐에서 데이터 디큐
int Peek(const Queue *q, int *x); // 맨 앞 데이터 확인
void Clear(Queue *q); // 모든 데이터 삭제
int Capacity(const Queue *q); // 큐 최대 용량 확인
int Size(const Queue *q); // 큐에 저장된 데이터 개수
int IsEmpty(const Queue *q); // 큐가 비어 있는지 확인
int IsFull(const Queue *q); // 큐가 가득 찼는지 확인
int Search(const Queue *q, int x); // 큐에서 데이터 검색
void Print(const Queue *q); // 큐 데이터 출력
void Terminate(Queue *q); // 큐 메모리 소멸
int main() {
Queue que;
int n;
printf("생성할 메모리 사이즈 : ");
scanf("%d", &n);
if(Create(&que, n) == -1) {
printf("큐 메모리 생성 실패\n");
}
while(1) {
int menu, x;
printf("현재 데이터 수 : %d / %d\n", Size(&que), Capacity(&que));
printf("(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : ");
scanf("%d", &menu);
if(menu == 0) {
break;
}
switch(menu) {
// 인큐
case 1:
printf("데이터 : ");
scanf("%d", &x);
if(Enque(&que, x) == 1) {
printf("인큐에 실패하였습니다.\n");
}
break;
// 디큐
case 2:
if(Deque(&que, &x) == -1) {
printf("디큐에 실패하였습니다.\n");
}
else {
printf("디큐한 데이터는 %d 입니다.\n", x);
}
break;
// 피크
case 3:
if(Peek(&que, &x) == -1) {
printf("피크에 실패하였습니다.\n");
}
else {
printf("피크한 데이터는 %d 입니다.\n", x);
}
break;
// 출력
case 4:
Print(&que);
break;
default:
printf("다시 입력해주세요.\n");
break;
}
}
Terminate(&que);
return 0;
}
// 큐 메모리 생성
int Create(Queue *q, int max)
{
if((q->que = malloc(sizeof(Queue) * max)) == NULL) {
q->max = 0;
return -1;
}
// if((q->que = calloc(max, sizeof(int))) == NULL) {
// q->max = 0;
// return -1;
// }
q->num = 0;
q->front = 0;
q->rear = 0;
q->max = max;
return 0;
}
// 큐에 데이터 인큐
int Enque(Queue *q, int x)
{
// 큐가 가득 찼을 경우
if(q->num >= q->max) {
return -1;
}
else {
q->num++; // 현재 요소 개수 증가
q->que[q->rear++] = x; // 요소 개수가 증가하여 리어 값도 같이 증가
// 리어 값이 최대 값이 되었을 때 리어 값을 0으로 초기화
if(q->rear == q->max) {
q->rear = 0;
}
return 0;
}
}
// 큐에서 데이터 디큐
int Deque(Queue *q, int *x)
{
// 큐가 비어 있을 경우
if(q->num <= 0) {
return -1;
}
else {
q->num--; // 현재 요소 개수 감소
*x = q->que[q->front++]; // 요소 개수가 감소하여 프론트 값 증가
// 프론트 값이 최대 값이 되었을 때 프론트 값을 0으로 초기화
if(q->front == q->max) {
q->front = 0;
}
return 0;
}
}
// 현재 꺼낼 데이터 확인
int Peek(const Queue *q, int *x)
{
// 큐가 비어 있을 경우
if(q->num <= 0) {
return -1;
}
*x = q->que[q->front]; // 현재 꺼낼 데이터 값
return 0;
}
// 모든 데이터 삭제
void Clear(Queue *q)
{
// 현재 요소 개수와 프론트 리어 모두 0으로 초기화
q->num = q->front = q->rear = 0;
}
// 큐 최대 사이즈
int Capacity(const Queue *q)
{
return q->max;
}
// 큐에 쌓여 있는 데이터 개수
int Size(const Queue *q)
{
return q->num;
}
// 큐가 비어 있는지 확인
int IsEmpty(const Queue *q)
{
return q->num <= 0;
}
// 큐가 가득 찼는지 확인
int IsFull(const Queue *q)
{
return q->num >= q->max;
}
// 큐에서 데이터 검색
int Search(const Queue *q, int x)
{
int i, idx;
for(i = 0; i < q->num; i++) {
idx = (i + q->front) % q->max;
//if(q->que[idx = (i + q->front) % q->max] == x) {
if(q->que[idx] == x) {
return idx; // 검색 성공
}
}
return -1; // 검색 실패
}
// 큐에 있는 모든 데이터 출력
void Print(const Queue *q)
{
int i;
for(i = 0; i < q->num; i++) {
printf("출력 데이터 [%d] %d\n", i, q->que[(i + q->front) % q->max]);
}
}
// 큐 메모리 소멸
void Terminate(Queue *q)
{
if(q->que != NULL) {
free(q->que);
}
q->max = q->num = q->front = q->rear = 0;
}https://github.com/JeHeeYu/Algorithm/tree/main/Queue
GitHub - JeHeeYu/Algorithm: 알고리즘 문제 풀이
알고리즘 문제 풀이. Contribute to JeHeeYu/Algorithm development by creating an account on GitHub.
github.com
실행 결과
생성할 메모리 사이즈 : 32
현재 데이터 수 : 0 / 32
(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : 1
데이터 : 4
현재 데이터 수 : 1 / 32
(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : 3
피크한 데이터는 4 입니다.
현재 데이터 수 : 1 / 32
(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : 1
데이터 : 5
현재 데이터 수 : 2 / 32
(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : 4
출력 데이터 [0] 4
출력 데이터 [1] 5
현재 데이터 수 : 2 / 32
(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : 2
디큐한 데이터는 4 입니다.
현재 데이터 수 : 1 / 32
(1)인큐 (2)디큐 (3)피크 (4)출력 (0)종료 : 0
요약 : Do it! 자료구조와 함께 배우는 알고리즘 입문: C 언어 편
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] C - 하노이의 탑(Towers Of Hanoi) (0) | 2022.11.12 |
|---|---|
| [Algorithm] C - 재귀함수(Recursion) (2) | 2022.11.12 |
| [Algorithm] C - 스택(Stack) (0) | 2022.11.07 |
| [Algorithm] C - 환형 더블 링크드 리스트(Circular Double Linked List) (0) | 2022.11.07 |
| [Algorithm] C - 더블 링크드 리스트(Double Linked List) (0) | 2022.11.06 |