요약
시간 복잡도 : O(n)
- 검색 방법 중 가장 단순하여 구현이 쉽움
- 정렬되지 않은 데이터 구조에서도 사용 가능
- 길이가 길수록 비효율(모든 데이터 검색 필요)
선형 검색(Linear Search)이란
선형 검색이란 데이터가 모인 집합(배열, 링크드 리스트 등)에서 원하는 키 값을 갖는 요소를 만날 때까지
맨 앞부터 순서대로 검색하여 찾는 검색 알고리즘을 말한다.
다른 말로 순차 검색(Sequential Search)라고도 한다.
검색하고자 하는 데이터 집합이 있다고 가정한다.
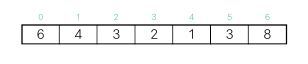
이 배열에서 2라는 값을 찾기 위해 0번 인덱스 요소부터 차례로 검색한다.

위 배열에서는 2라는 값을 찾기 위해 4번의 검색으로 발견하였다.
- 첫 번째 인덱스 값 6 확인, 원하는 값이 아님
- 두 번째 인덱스 값 4 확인, 원하는 값이 아님
- 세 번째 인덱스 값 3 확인, 원하는 값이 아님
- 네 번째 인덱스 값 2 확인, 원하는 값 확인
하지만, 찾고자 하는 값이 배열에 존재하지 않을 경우, 모든 배열을 검색하여야 한다.
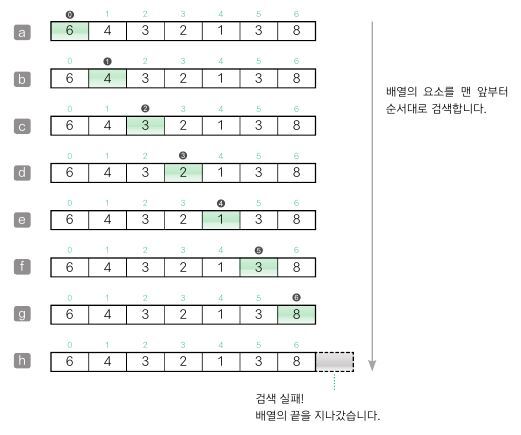
즉, 선형 검색의 종료 조건은 2가지로 정리할 수 있다.
- 검색할 값을 발견하지 못하고 배열의 끝까지 확인한 경우
- 검색할 값을 발견한 경우
이렇게 발견하지 못했을 경우 모든 배열을 확인해야 해서 많은 비용이 드는 것을 볼 수 있다.
이러한 비용을 반으로 줄일 수 있는 방법이 있는데, 그 방법을 보초법 이라고 한다.
보초법(Sentinel Method)
보초법이란 반복의 종료를 알리는 특정한 값인 보초(Sentinel) 값을 사용하여 종료 조건 중 검색 실패 조건을 제거하여
판단(비용) 횟수를 줄이는 방법을 말한다.
어떤 배열을 검색하기 전에 검색하고자 하는 키 값을 배열의 맨 끝 요소에 저장한다. (이것이 보초)

보초법을 적용하면 원하는 값이 배열에 존재하지 않아도 보초까지 검색하면 종료 조건이 달성되어 종료한다.
보초는 반복문에서 종료 판단 횟수를 2회에서 1회로 줄이는 역할을 한다.
예제 코드
#include <stdio.h>
#include <stdlib.h>
// a : 배열, n : 요소 개수, key : 찾고자 하는 값
int LinearSearch(int *a, int n, int key)
{
int i = 0;
// 배열의 마지막 요소에 보초 추가
a[n] = key;
while(1) {
if(a[i] == key) {
break;
}
i++;
}
// 배열의 끝까지 검색했을 때 못찾으면 -1을 리턴
return i == n ? -1 : i;
}
int main()
{
int i, n, key, index;
int *x;
printf("요소 개수 : ");
scanf("%d", &n);
x = malloc(sizeof(int) * n);
for(i = 0; i < n; i++) {
printf("x[%d] : ", i);
scanf("%d", &x[i]);
}
printf("검색 값 : ");
scanf("%d", &key);
index = LinearSearch(x, n, key);
if(index == -1) {
printf("검색 실패!\n");
}
else {
printf("%d = x[%d]에 있음\n", key, index);
}
free(x);
}실행 결과
요소 개수 : 7
x[0] : 6
x[1] : 4
x[2] : 3
x[3] : 2
x[4] : 1
x[5] : 3
x[6] : 8
검색 값 : 3
3 = x[2]에 있음
요소 개수 : 7
x[0] : 6
x[1] : 5
x[2] : 1
x[3] : 9
x[4] : 7
x[5] : 6
x[6] : 4
검색 값 : 8
검색 실패!https://github.com/JeHeeYu/Algorithm/tree/main/Search/Linear%20Search
GitHub - JeHeeYu/Algorithm: 알고리즘 개념 및 문제 풀이
알고리즘 개념 및 문제 풀이. Contribute to JeHeeYu/Algorithm development by creating an account on GitHub.
github.com
출처 : Do it! 자료구조와 함께 배우는 알고리즘 입문: C 언어 편
'Algorithm > 이론' 카테고리의 다른 글
| [Algorithm] C - 퀵 정렬(Quick Sort) (0) | 2022.11.14 |
|---|---|
| [Algorithm] C - 이진 탐색(Linear Search) (0) | 2022.11.14 |
| [Algorithm] C - 삽입 정렬(Insertion Sort) (0) | 2022.11.12 |
| [Algorithm] C - 선택 정렬(Selection Sort) (0) | 2022.11.12 |
| [Algorithm] C - 버블 정렬(Bubble Sort) (0) | 2022.11.12 |